libecc: Elliptic Curve Cryptography C++ Library

Main Page Reference Manual Compound List File List

Introduction

Galois field

In this chapter it is assumed that you've read and understood the theory of the Galois field $\mathbb{F}_{2^m}$ (in literature also often denoted with GF(2^m)). In particular the fact that such a field has a finite number of elements (namely 2^m, also called the size, order or cardinality of the field) and that the properties of the field are solely determined by this cardinality: any two fields with the same number of elements are isomorphic (that means that there is a one-on-one relationship between all the elements of the two fields (called a bijective map) that retains the additive and multiplicative relationships). Most notably, every element E of the field has one and only one solution S to the equation S² = E. 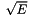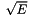This is a result of having characteristic 2; normally one would expect to have two solutions: + $\sqrt{E}$ and - $\sqrt{E}$ , but since -1 $\equiv$ +1 those are the same and we only have one solution.

The cardinality of the Galois field 2^m (the number of elements in it), is not to be confused with what is known as the field characteristic. The field characteristic is 2, in this case. The meaning of the characteristic of finite fields, usually denoted with p, is that it is the smallest positive integer for which pE = 0 for every element E of the field. 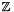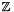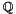This characteristic is noted down with p because it is always prime for finite fields (Note that in the case of fields with a ground field (also called base field, or prime field; in our case it is $\mathbb{Z}$ ₂, in the more general case it is either $\mathbb{Z}$ _p or $\mathbb{Q}$ ) of infinite cardinality (thus with ground field 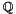$\mathbb{Q}$ ) the characteristic is said to be 0, not infinite). It is easy to derive this: Let K be a field with characteristic p. Then if it were possible to write p = qr with q and r integers larger than 1, then there has to exist an element A for which B = qA 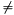$\neq$ 0 (otherwise q would be the characteristic) and an element C for which D = rC 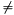$\neq$ 0. Furthermore, D must have an inverse because it is element of a field: DD^-1 = 1. From that follows that 0 = p ACD^-1 = qr ACD^-1 = qA rC D^-1 = B DD^-1 = B 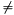$\neq$ 0, which is a contradition.

Because the cardinality of the Galois field plays an important role we will assign a special character for it. In the literature often the letter q is used. Let therefore q = 2^m from now on.

Elliptic curves, solutions, points and cardinality

Every elliptic curve (for any a and b) of the form x³ + ax² + b = y² + xy over 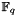$\mathbb{F}_q$ , will have solutions. The question is: how many solutions? How many points (x,y) will exist, on a given curve?

In an artificial way, it is possible to define a binary operator that assigns a third point on the curve to a combination of two other points. It is needed to add one artificial point, that is not a solution of the curve, if we want to make the complete set of points an Abelian Group.

An Abelian group is a group of elements with a binary operator that is commutative. For example, let p, r and s be points on the curve and (p, r) $\rightarrow$ s then also (r, p) $\rightarrow$ s (commutation axioma). The extra point that is not a solution of the curve, is the identity (if we denote this element with an e, then (p, e) $\rightarrow$ p for every point p on the curve). 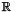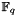This point is also called "the point at infinity" because it would make sense to think of it like that when constructing the binary operator in a graphical way over the field of real numbers $\mathbb{R}$ (as opposed to over $\mathbb{F}_q$ ).

The artificial way in which this binary operator is constructed is not relevant once we know the structure of the (finite and commutative) group. Those are implementation details that were only relevant while writing the library and during the analysis of a curve to derive its structure in another way than by brute force determining the order of its points. The C++ library overloads operator+ for the binary operator of the Abelian group of points. The identity element is therefore refered to as zero in the source code. It is common to use the additive operator for an Abelian group, but we might as well have used operator*, or any other binary operator.

Just as is the case with Galois fields, the number of elements (number of points on the curve (including the zero), or solutions of the curve (combined with the additive identity); also called the order of the curve E( 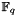$\mathbb{F}_q$ ), or #E( 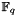$\mathbb{F}_q$ ), and equal to the cardinality (or even 'power' in older books) of the Abelian group formed by those points) is a measure for the characteristics of the Abelian group formed by these points - and therefore its security for cryptographic purposes. Below we will talk about 'the cardinality of a curve' instead of 'the order of a curve', so that there can be less confusion about the meaning of the word 'order', which we will frequently use for the order of a point.

From now on we will speak about points instead of solutions, but it means the same. However, if we speak about points than we include the 'point at infinity', the additive identity, the zero. This just makes most sense because then 'the number of points on a curve' is equal to the cardinality of the finite Abelian group formed by the points. In other words, when we speak about 'the number of ...' then we always include the additive identity, except perhaps when we specifically talk about 'the number of solutions' (of an equation).

Adding or multiplying points?

As is said, it is common to use addition as binary operator for an Abelian group: (G,+). Most theory about elliptic curves as well as the interface of libecc will use the + sign to denote the binary operator.

Using multiplication or addition as binary group operator is just a semantic issue. When using multiplication as binary operator then it becomes clear why the difficult-to-solve mathematical problem, on which elliptic curve cryptography is based, is called the Discrete Logarithmic Problem. The problem refered to here is solving n from the equation p * p * p * ... * p = pⁿ = r, where p and r are points on the curve and n is a large integer. Equivalent however, when we use addition as the binary group operator, is solving n from the equation p + p + p + ... + p = np = r.

Point counting

The number of solutions to the elliptic curve x³ + ax² + b = y² + xy over 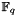$\mathbb{F}_q$ is obviously finite because there are only a finite number of possible values for x and y. Since both x and y can each only be one of q values, the total number of possible combinations (x,y) is q². Not all those possibilities will actually be solutions to the curve of course. If that where the case then we'd have a "2-dimensional" area, black with points. Instead we have a curve, a line, that runs through this space and we merely expect to have a "1-dimensional" number of points on that curve, of the order of q plus or minus some variation.

In fact, we can set a much stricter interval for the number of points on the curve. After all, the maximum number of possible solutions is two for each possible value of x. For any given x 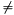$\neq$ 0, y is given by a quadractic equation with zero or two solutions. If y₁ is a solution of the quadratic equation y² + xy + c = 0 (where c = x³ + ax² + b), then y₂ = y₁ + x is also a solution, what can easily be shown by filling in y₂ into the equation and recalling the fact that (u + v)² = u² + v² and u² + u² = 0, for any polynomials u and v.

The brute force way to count the number of points on a given elliptic curve is by trying to solve the quadratic equation for y, for every possible value of x. x = 0 always has a single solution: 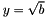$y=\sqrt{b}$ . All other values of x will have either none or two solutions.

We can picture this with a "matrix" representation, plotting x horizontally and y vertically. For example, the curve with m=4, reduction polynomial t⁴ + t + 1 = 0, a = t³ + t + 1 and b = t has the following solutions:

15  - - - - - - - - - - - - - - - -
14  - - - - - - - - - - - - - - - -
13  - - - - - - - - - - - - - X - -
12  - - - - - - - - X - - X - - - -
11  - - - - - - - - - - - - - - - -
10  - - - - - - - - - - - - X - - -
 9  - - - - - - - - - - - - - - - -
 8  - - - - - - - - - - - - - - - -
 7  - - - - - - X - - - - X - - - -
 6  - - - - - - - - - - - - X - - -
 5  X - - - - - - - - - - - - - - -
 4  - - - - X - - X X - - - - - - -
 3  - - - - - - - X - - - - - - - -
 2  - - X - - - - - - - - - - - - -
 1  - - - - - - X - - - - - - - - -
 0  - - X - X - - - - - - - - X - -

    0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1
    0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5

Don't be confused about the decimal numbers 0 through 15, they represent the 2⁴ polynomials of the Galois field as follows: write them in binary, then bit n represents tⁿ. For example, as said before we always have the point (0, 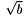$\sqrt{b}$ ), which is represented by the X in the left most column in this maxtrix. Apparently 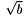$\sqrt{b}$ = 5. 5 in binary is 101 and therefore represents t² + 1. If we square this we should get b = t back; (t² + 1)² = t⁴ + 1 = t (the irreducible polynomial of degree 4 used is t⁴ + t + 1, so t⁴ = t + 1). There is more that we can recognize in this matrix. As was derived above, every non-zero value of x has exactly zero or two solutions (the y₁ and y₂ mentioned above). We clearly see this back in the matrix because each of the 15 columns on the right have either zero or two Xs in them. Note that the definition for addition of points tells us that - (x, y₁) = (x, y₁ + x), and thus (x, y₁) + (x, y₂) = 0.

Likewise, every row has zero, one, two or three Xs in them. This is obviously because those are solutions of the cubic equation x³ + ax² + yx + (b + y²) = 0 (are you getting used yet to fields with characteristics 2 where addition and subtraction are the same?). Finally there is one more property of the (x, y) solutions that is immediately visible from this matrix: the distance between every two Xs in one column is equal to the value of the x coordinate. This is of course a direct result of the fact that y₁ = y₂ + x. Please remember that adding two polynomials has to be done 'bitwise' modulo 2, in other words you have to use the XOR operator for addition (and subtraction), like explained in the chapter about polynomials. The fact that in most cases of this example (namely all of them except x = 7) you can simply add the decimal representation of the y values with x and then subtract 16 from the result if needed (wrap vertically around) is a coincidence! Examples for which this won't work are 3 + 7 = 4 (the column with x = 7; (t + 1) + (t² + t + 1) = t²) and 2 + 6 = 4 (t + (t² + t) = t²). Just use exclusive-OR for addition, as has been explained in the theory about of the polynomials , and you'll be fine.

Brute force results

Brute force counting the points on an elliptic curve is only feasible for very small q. We counted the number of points for every possible combination of a and b, with m = 3, 4, 5, 6, 7, 9 and 10. The program used to do this can be found in testsuite/point/pointTest.cc. The graphs below show the results.

These are the results for the elliptic curves over the field $\mathbb{F}$ _2³ with reduction polynomial t³ + t + 1.

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 56.

There are 4 combinations of a and b for which the resulting curve has 3 solutions, including the zero point that makes 4 points; the cardinality of those 4 curves is thus 4. 12 curves have a cardinality of 6, 12 curves have a cardinality of 8, 12 curves have a cardinality of 10, 12 curves have a cardinality of 12 and 4 curves have a cardinality of no less than 14.

The structure of (the finite, Abelian group formed by the points on) every elliptic curve turns out to be cyclic, and therefore all curves with the same number of points on them have the same properties. They are said to be isogenous.

Note that gcd(4, 12) = 4 = q/2.

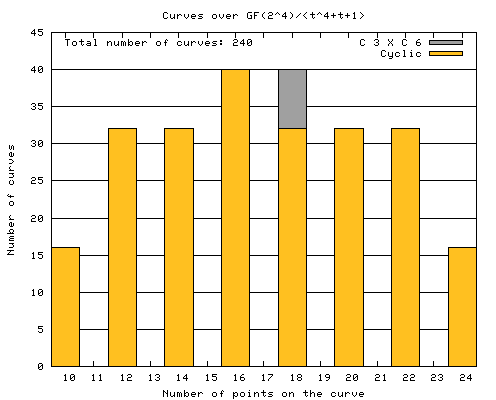These are the results for the elliptic curves over the field $\mathbb{F}$ _2⁴ with reduction polynomial t⁴ + t + 1.

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 240.

There are 16 combinations of a and b for which the points of resulting curve form an Abelian group with a cardinality of 10. There are every time 32 curves that have respectively a cardinality of 12, 14, 20 or 22, 40 curves have a cardinality 16 or 18 and 16 curves have a cardinality of no less than 24.

In this case not every elliptic curve is cyclic. The structure of 8 curves turns out to be C₃ $\times$ C₆. That structure has 18 elements, but it is not isomorphic with the cyclic (one dimensional) C₁₈.

Note that gcd(8, 16, 32, 40) = 8 = q/2.

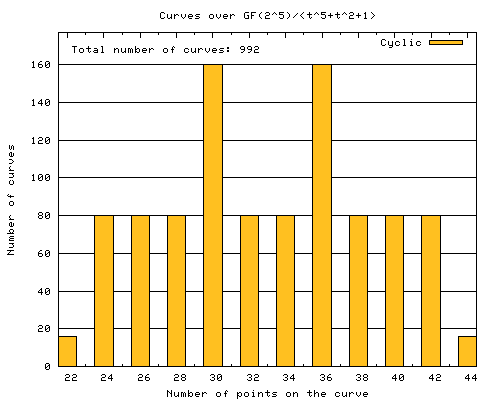These are the results for the elliptic curves over the field $\mathbb{F}$ _2⁵ with reduction polynomial t⁵ + t² + 1.

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 992.

There are 16 combinations of a and b for which the resulting curve has a cardinality of 22. There are every time 80 curves that have cardinality of respectively 24, 26, 28, 32, 34, 38, 40 and 42. 160 curves have cardinality 30 or 36 and 16 curves have a cardinality of no less than 44.

Again, it turns out that every curve leads to a cyclic structure.

Note that gcd(16, 80, 160) = 16 = q/2.

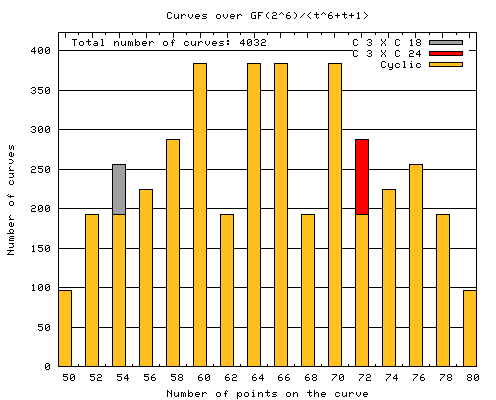These are the results for the elliptic curves over the field $\mathbb{F}$ _2⁶ with reduction polynomial t⁶ + t + 1. Also t⁶ + t³ + 1 is irreducible, but we can ignore variations in k because it will have absolutely no influence on any property or characteristic of the resulting elliptic curve: the result is isomorphic.

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 4032.

The exact values of the data is given in the table below.

Note that gcd(64, 96, 192, 224, 256, 288, 384) = 32 = q/2.

Number of points on the curve	50	52	54	56	58	60	62	64	66	68	70	72	74	76	78	80
Number of cyclic groups	96	192	192	224	288	384	192	384	384	192	384	192	224	256	192	96
Number of C₃ X C₁₈			64
Number of C₃ X C₂₄												96

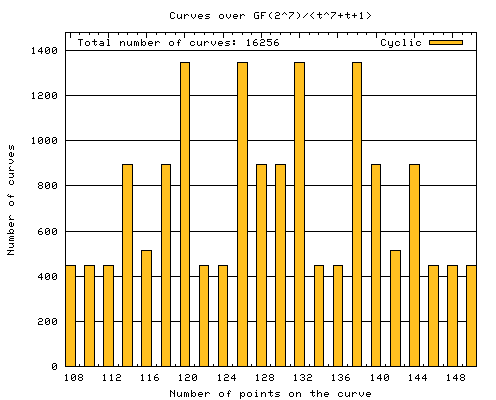These are the results for the elliptic curves over the field $\mathbb{F}$ _2⁷ with reduction polynomial t⁷ + t + 1 (or t⁷ + t³ + 1 that gives the exact same results).

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 16256.

The exact values of the data is given in the table below.

Note that gcd(448, 512, 896, 1344) = 64 = q/2.

Number of points on the curve	108	110	112	114	116	118	120	122	124	126	128
Number of cyclic groups	896	1344	448	448	1344	896	512	896	448	448	448
Number of points on the curve	130	132	134	136	138	140	142	144	146	148	150
Number of cyclic groups	448	448	448	896	512	896	1344	448	448	1344	896

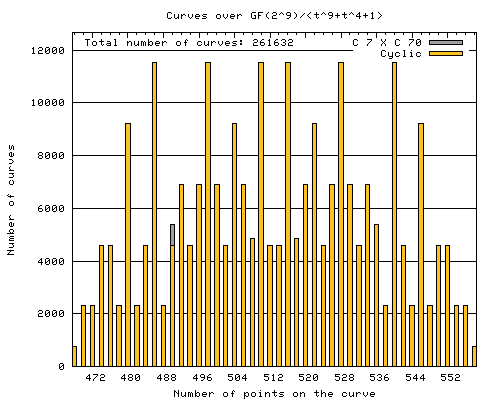These are the results for the elliptic curves over the field $\mathbb{F}$ _2⁹ with reduction polynomial t⁹ + t⁴ + 1 (or t⁹ + t + 1 with the same results).

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 261632.

The exact values of the data is given in the table below.

Note that gcd(768, 2304, 4608, 4864, 5376, 6912, 9216, 11520) = 256 = q/2.

Number of points on the curve	468	470	472	474	476	478	480	482	484	486	488	490
Number of cyclic groups	768	2304	2304	4608	4608	2304	9216	2304	4608	11520	2304	4608
Number of C₇ X C₇₀												768
Number of points on the curve	492	494	496	498	500	502	504	506	508	510	512	514
Number of cyclic groups	6912	4608	6912	11520	6912	4608	9216	6912	4864	11520	4608	4608
Number of points on the curve	516	518	520	522	524	526	528	530	532	534	536	538
Number of cyclic groups	11520	4864	6912	9216	4608	6912	11520	6912	4608	6912	5376	2304
Number of points on the curve	540	542	544	546	548	550	552	554	556	558
Number of cyclic groups	11520	4608	2304	9216	2304	4608	4608	2304	2304	768

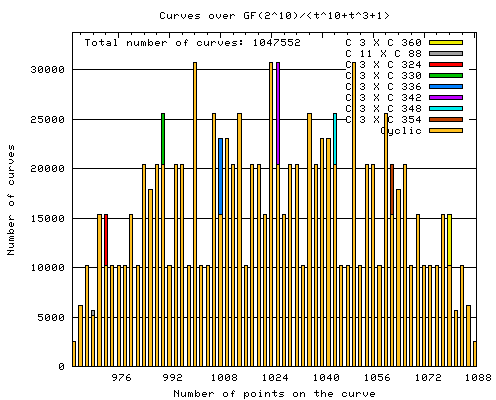These are the results for the elliptic curves over the field $\mathbb{F}$ _2¹⁰ with reduction polynomial t¹⁰ + t³ + 1.

Every possible value of a and b except b = 0 has been calculated. The total number of elliptic curves is therefore q(q-1) = 1047552.

The exact values of the data is given in the table below.

Note that gcd(512, 2560, 5120, 5632, 6144, 7680, 10240, 15360, 17920, 20480, 23040, 25600, 30720) = 512 = q/2.

Number of points on the curve	962	964	966	968	970	972	974	976	978	980	982	984
Number of cyclic groups	2560	6144	10240	5120	15360	10240	10240	10240	10240	15360	10240	20480
Number of C₁₁ X C₈₈				512
Number of C₃ X C₃₂₄						5120
Number of points on the curve	986	988	990	992	994	996	998	1000	1002	1004	1006	1008
Number of cyclic groups	17920	20480	20480	10240	20480	20480	10240	30720	10240	10240	25600	15360
Number of C₃ X C₃₃₀			5120
Number of C₃ X C₃₃₆												7680
Number of points on the curve	1010	1012	1014	1016	1018	1020	1022	1024	1026	1028	1030	1032
Number of cyclic groups	23040	20480	25600	10240	20480	20480	15360	30720	20480	15360	20480	20480
Number of C₃ X C₃₄₂									10240
Number of points on the curve	1034	1036	1038	1040	1042	1044	1046	1048	1050	1052	1054	1056
Number of cyclic groups	10240	25600	20480	23040	23040	20480	10240	10240	30720	10240	20480	20480
Number of C₃ X C₃₄₈						5120
Number of points on the curve	1058	1060	1062	1064	1066	1068	1070	1072	1074	1076	1078	1080
Number of cyclic groups	10240	25600	15360	17920	20480	10240	15360	10240	10240	10240	15360	10240
Number of C₃ X C₃₅₄			5120
Number of C₃ X C₃₆₀												5120
Number of points on the curve	1082	1084	1086	1088
Number of cyclic groups	5632	10240	6144	2560

Conclusions

From this brute force data we can already draw some remarkable conclusions. First of all, it is clear that any isomorphic group of curves comes in batches of q/2 at a time. Because this amount is of the order of q we can conclude that there is probably a relationship between a and b that expresses one in the other (so that the total number of 'interesting' curves is reduced from q² to about q), my poor PC is going to like that when we will continue to explore curves of a higher cardinality.

Secondly, there is a striking symmetry between curves of a cardinality #E( 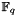$\mathbb{F}_q$ ) and 2(q + 1) - #E( 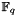$\mathbb{F}_q$ ) : there exists exactly the same number of combinations of a and b for either of the two cardinalities! We can expect to also see this pairing of cardinality back in a symmetry of a and b.

Actually, since we omitted the value b = 0 (because the resulting equations do not give rise to an Abelian group), there are an even number (q) of possible values for a and an odd number (q - 1) of possible values for b. That makes it likely that the batches of isomorphic curves are generated by a variation of a only, where exactly half of the values of a lead to isomorphic curves while the other half then might correspond with the cardinality "mirrored" in q + 1.

This hypothesis can easily be checked. For each combination of a and b that results in the a curve with the same structure, we check that there are exactly q/2 different values of a being used and that each of those values is combined with the same set of values of b. 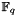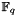Moreover, we check that for the other q/2 values of a while keeping the value of b constant, the cardinality changes from #E( $\mathbb{F}_q$ ) into 2(q + 1) - #E( $\mathbb{F}_q$ ).

This (and more, see below) is tested by the program testsuite/point/plot.cc. The hypothesis turns out to be correct; at least emperically, for m 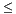$\leq$ 10.

We can make this investigation more accessible by making it visible as follows. The matrix below shows the simplest case, where m = 3 and thus q = 2^m = 8. Horizontally all values of a are plotted (left to right, 0 to 7) against vertically all values of b (bottom to top, 1 to 7. The black bar at the bottom corresponds with b = 0 for which there are no curves). Again, and this is the last time that I mention it, the convention was used that each bit of these values represent a coefficient of the polynomial field; for example, a value of 6 corresponds to t² + t etc. As such, each of the 56 little squares corresponds to one possible curve over F_2³. Furthermore, each different structure of the Abelian groups that these curves give rise to is given a different color.

And indeed we see the following properties:

Each row contains exactly two colors, q/2 of each.
Those two colors correspond to structures with 'opposite' cardinality (that is, if you add the cardinalities then you get 2(q + 1)).
Each row having the same two colors shows the exact same pattern. This means that the structure in a is not a function of b.

There is another symmetry that we see now, which goes behond the hypothesis that I deduced from the point counting data. It shows that the structure in a (the pattern of the two colors per row) is even the same for different structures! This means that the structure of a is entirely independent of b and only a function of m. The data below for larger m (and the program testsuite/point/plot.cc) confirms this.

The question that now arrises is of course: how is this structure of a depending on m? A first guess, from the above matrix with m = 3 could be that the color alternates when we add 1 (meaning that the bit that corresponds to 1, and that bit only, determines the structure of the curve (apart from the value of b of course). However, that turns out to be a bit too simple as can already been seen from the data with m = 4: