libecc: Elliptic Curve Cryptography C++ Library

Main Page Reference Manual Compound List File List

On this page I will analyse the factorization of 2^m - 1. This page is not in chronological order.

Chronological History

On January 12th 2007, I wrote down the factorization of 2^m - 1 for m=2...16 because I was interested to see where a factor of the form 2ⁿ + 1 would appear. I took the piece of paper to bed with me, to study it, when suddenly I saw structure (conjecture 1, with n equal zero). I got out of bed again and copied the factorization of 2^m - 1 for m=17...36 as well. Back in bed, I verified that my conjecture still held and discovered the structure of conjecture 1 with n=1 (and a single data point with n=2). I studied the remaining factors and discovered they all had the form (c m + 1) (conjecture 2). I didn't sleep much that night.

The next day I wrote a program (factorization2.cc) that used conjecture 1, and refined this conjecture in it's current form (still without proof). Then I extended the program to find the factorization of the remaining factors using brute force, which worked extremely fast till m=58 and reached m=82 over night. Studying 2¹¹ - 1, I realized that the binomial expansion of (1+1)¹¹ might be relevant and I thought that if I understood why the remaining factors were all of the form (c m + 1) then I might discover a way to find those factors a lot faster. In the next few days I extended the program to use the Cunningham tables in order to have the factors up till 2⁷⁸⁷ - 1 available, giving me a large control set. I also proved conjecture 1 to hold for n=0 and n=1.

Larger values turned out to be very hard to prove. I downloaded a trial version of Mathematica on January 17th, and started to learn how to use it. After a few days I could calculate the remainder of (x^km - 1) / (x^m - 1)ⁿ, but only for fixed values of k, m and n. Nevertheless, by using a few prime values for m and very large values for k, I was able to guess a form for the remainders as polynomials in k for n=2...6. This remainder contained a lot of fixed numbers that I couldn't place for several days until finally I plotted the polynomials of k, that I had fit to the data, and found that for constant n they all crossed the same n+1 points. Rearranging things a bit I then formulated the "Pink polynomials" and the next couple of days derived a general form for them.

Having this general form, I was able to prove the correctness of conjecture 1 for n=2...5. A day later I added the last part and finished the proof for arbitrary n. Conjecture 1 was now proved. This was today January 23th, at which point I started to write this document. Anything else will be chronological, adding it as I move forwards.

The actual proof of conjecture 1 is impossible if you do not first know the answer. It took three weeks to find that answer (it is now Februari 17th). It would take too long to show the path followed that lead to the answer. However, I wish to thank Neil Sloane for an important contribution that led to this result, by finding a way to generate a pyramid of integers that I had generated along the way.

A simple pattern

CONJECTURE 1

Let k, m, n be non-negative integers, x an integer larger than 0, and p prime. If $p \mid x^m-1$ and $p^n \mid k$ then $p^{n+1} \mid x^{km}-1$ .

PROOF

If x = 1, k = 0 or m = 0 there is nothing to prove. Therefore consider the case where x > 1, k > 0 and m > 0.

Let u = x^m, thus u > 1. It won't be used that u is a power of x until at the end of the proof.

Let n be a non-negative integer, and recall that

$(u-1)^n = \sum_{j=0}^n{(-1)^{n-j}\binom{n}{j}u^j}$

(1)

and

$\frac{u^k-1}{u-1} = \sum_{i=0}^{k-1}{u^i}$

(2)

Consider the equation

$u^k-1 = (u-1)^{n+1} \sum_{i=0}^{k-n-1}{\binom{k-1-i}{n}u^i} + (u-1)R_{n,k}(u)$

(3)

which defines the function R_n,k(u),

$R_{n,k}(u) = \frac{u^k-1}{u-1} - (u-1)^n \sum_{i=0}^{k-n-1}{\binom{k-1-i}{n}u^i}$

(4a)

Using (1), we can work out the sum

$\begin{split} (u-1)^n \sum_{i=0}^{k-n-1}{\binom{k-1-i}{n}u^i} &= \sum_{j=0}^n{(-1)^{n-j}\binom{n}{j}u^j} \sum_{i=0}^{k-n-1}{\binom{k-1-i}{n}u^i} \\ &= \sum_{j=0}^n{\sum_{i=0}^{k-n-1} (-1)^{n-j} \binom{n}{j} \binom{k-1-i}{n} u^{i+j}} \end{split}$

(5a)

This sums over 0 <= j <= n and 0 <= i < k-n.

What we'd like is to sum over i+j. Let r = i+j with a total range of 0 <= r < k. Because the binomial $\binom{n}{j}$ is zero for values of j < 0 and j > n, we can savely replace the sum over j with a sum over r, so that (5a) becomes,

$\sum_{r=0}^{k-1}{\left(\sum_{i=0}^{k-n-1}(-1)^{n-(r-i)}\binom{n}{r-i}\binom{k-1-i}{n}\right)u^r}$

(5b)

Where the first binomial will be non-zero only when 0 <= r-i <= n and the second binomial will be non-zero only when n <= k-1-i. In otherwords, the only non-zero terms are those when max(0,r-n) <= i <= min(r,k-n-1). If k-n-1 < r but we sum till r anyway, then this is no problem because for values of i > k-n-1, the second binomial is zero anyway. Therefore we can sum over max(0,r-n) <= i <= r. This then suggests we should split the sum into two parts, one where r < n and one where r >= n.

$\sum_{r=0}^{n-1}{\left(\sum_{i=0}^{k-n-1}(-1)^{n-(r-i)}\binom{n}{r-i}\binom{k-1-i}{n}\right)u^r}+ \sum_{r=n}^{k-1}{\left(\sum_{i=r-n}^r(-1)^{n-(r-i)}\binom{n}{r-i}\binom{k-1-i}{n}\right)u^r}$

(5c)

Using the identity $\sum_k\binom{n}{k}\binom{r-sk}{n}(-1)^k=s^n\text{,}\quad\text{integer $n \ge 0$}$ [KNUTH, 5.43], we can rewrite the inner sum of the second term as

$\sum_{i=r-n}^r(-1)^{n-(r-i)}\binom{n}{r-i}\binom{k-1-i}{n} = \sum_{i=0}^n(-1)^i\binom{n}{i}\binom{k-1-r+n-i}{n} = 1^n = 1$

(6)

Now we can rewrite (4), using (2), (5c) and (6) to read

$\begin{split} R_{n,k}(u) &= \sum_{i=0}^{k-1}{u^i}- \left\{\sum_{r=0}^{n-1}{\left(\sum_{i=0}^{k-n-1}(-1)^{n-(r-i)}\binom{n}{r-i}\binom{k-1-i}{n}\right)u^r} + \sum_{r=n}^{k-1}{u^r}\right\} \\ &= \sum_{i=0}^{n-1}{\left(H[k-1-i] - \sum_{j=0}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n}\right)u^i} \end{split}$

(4b)

where $H[n]$ is the Heaviside step function,

$H[k-1-i] = \begin{cases}0 &\text{if $k \le i$}\\1 &\text{if $k > i$}\\\end{cases}$

(7)

Define for non-negative k and 0 <= i < n, the family of functions

$P_{i,n}(k) = H[k-1-i] - \sum_{j=0}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n}\quad\quad\text{if $k \ge 0$}$

(8)

Then we can write R_n,k(u) as

$R_{n,k}(u) = \sum_{i=0}^{n-1} P_{i,n}(k) u^i$

(4c)

Note that because the sum in (8) is empty for k <= n, we found that

$P_{i,n}(k) = \begin{cases} 0 & 0 \le k \le i \\ 1 & i < k \le n \\ \end{cases}$

(9)

We can rewrite the sum in (8) a bit. Note that, using [KNUTH, 5.43] again,

$\begin{split} \sum_{j=i-n}^{i}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} &= (-1)^n \sum_{j=0}^{n}(-1)^{j}\binom{n}{j}\binom{k-1-i-((-1)j)}{n} = (-1)^n (-1)^n = 1 \end{split}$

(10)

and thus, if k-n-1 <= i,

$\begin{split} \sum_{j=i-n}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} &= 1 - \sum_{j=k-n}^{i}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} \end{split}$

(11)

Then note that the value of k-1-j in the last binomial factor of the last sum is maximal when j is minimal. This minimal value is k-n, thus the maximum value of the k-1-j is k-1-(k-n) = n-1, rendering this binomial, and therefore the whole sum, zero provided that k-1-j >= 0 for all values of j. The minimal value of k-1-j is obtained for j = i, so that we can conclude that the second sum is zero if k > i.

While if k-n-1 >= i then (10) can be written as

$\sum_{j=i-n}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} = 1 + \sum_{j=i+1}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} = 1$

(12)

because $\binom{n}{i-j} = 0$ for all values of j.

Hence, we have

$\begin{split} \sum_{j=i-n}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} &= \begin{cases} 0 & \text{if $k \le i$ (because then the sum is empty)} \\ 1 & \text{if $ k > i$} \end{cases} \\ &= H[k-i-1] \end{split}$

(13)

And, with k >= 0, we can write (8) as

$\begin{split} P_{i,n}(k) &= \sum_{j=i-n}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} - \sum_{j=0}^{k-n-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} \\ &= \sum_{j=i-n}^{-1}(-1)^{n-(i-j)}\binom{n}{i-j}\binom{k-1-j}{n} \\ &= \sum_{j=0}^{n-1-i}(-1)^{j}\binom{n}{j}\binom{k-1-j-i+n}{n} \end{split}$

(14)

Lets try to write P_i,n(k) as a finite sum of powers of k. We can find the highest power by using the finite difference method. This method shows that we can write a sequence as a polynomial of degree n, if the n-th difference gives a constant sequence. As we can learn from this wikipedia reference about the n-th difference operator , there exists a formula that will give us directly the d-th difference:

$\Delta^d [P_{i,n}](k)= \sum_{r=0}^d (-1)^{d-r} \binom{d}{r} P_{i,n}(k+r)$

(15)

Because of (9) we known that the degree is at least n. Experimentally fitting polynomials to calculated data gives polynomials of exactly degree n that are correct up till very large k. This motivates us to try d = n and calculate $\Delta^n [P_{i,n}](0)$ , using (9) and the identity $\sum_{j=0}^{k} (-1)^j{n\choose j} = (-1)^k{n-1\choose k}$ from wikipedia for the last step, to get

$\begin{split} \Delta^n [P_{i,n}](0) &= \sum_{r=0}^n (-1)^{n-r} \binom{n}{r} P_{i,n}(r) \\ &= \sum_{r=0}^n (-1)^{n-r} \binom{n}{r} H[r-1-i] \\ &= \sum_{r=i+1}^n (-1)^{n-r} \binom{n}{r} \\ &= \sum_{r=i+1}^n (-1)^{n-r} \binom{n}{n-r} \\ &= \sum_{r=0}^{n-1-i} (-1)^r \binom{n}{r} \\ &= (-1)^{n-1-i} \binom{n-1}{i} \end{split}$

(16)

If this is to be a constant (with fixed i and n) for larger values of k, then we have proven that P_i,n(k) can actually be written as a polynomial in k of degree n. That is, we have to show that for k >= n, $P_{i,n}(k) = \hat{P}_{i,n}(k) = D_{i,n}(0,k)$ , where $D_{i,n}(d,k) = \Delta^d [\hat{P}_{i,n}](k)$ is given by the recurrence

$\begin{aligned} D_{i,n}(n,k) &= (-1)^{n-1-i} \binom{n-1}{i} \\ D_{i,n}(d,n-d) &= \Delta^d [P_{i,n}](n-d) \\ D_{i,n}(d-1,k+1) &= D_{i,n}(d-1,k) + D_{i,n}(d,k) \end{aligned}$

(17)

As follows directly from (9), $\Delta^0 [P_{i,n}](n-0) = P_{i,n}(n) = 1$ . In fact, P_i,n(k) = 1, if i < k <= n, and as follows directly from (15), $\Delta^d [P_{i,n}](k)$ depends only on the values of P_i,n(r) with k <= r <= k+d, so that $\Delta^d [P_{i,n}](n-d) = 0$ , if i < n-d <= n. Moreover, as also follows directly from (9), P_i+1,n+1(k+1) = P_i,n(k), for 0 <= k <= n, because if you add one to k and n then k is still less than or equal n so that (9) still holds, and H[k-1-i] doesn't change. Thus we have the identity $\Delta^d [P_{i+1,n+1}](k+1) = \Delta^d [P_{i,n}](k)$ , if 0 <= k <= n - d, which translates into $\Delta^d [P_{i,n}](n-d) = \Delta^d [P_{i-(n-d),n-(n-d)}](n-d-(n-d)) = \Delta^d [P_{i-(n-d),d}](0)$ , if d > 0 and i >= n-d. Note that d = 0 fails because (9) demands that i < n, thus n > 0, and (16), which we'll need, puts d = n. Combining, we find that

$\Delta^d [P_{i,n}](n-d) = \begin{cases} 1 & \text{if $d = 0$} \\ 0 & \text{if $d > 0$ and $i < n-d$} \\ \Delta^d [P_{i-(n-d),d}](0) & \text{if $d > 0$ and $i \ge n-d$} \end{cases}$

(18)

Thus, using (16), and realizing that $\binom{d-1}{i-(n-d)} = 0$ if d > 0 and i < n - d, we can rewrite (17) as

$\begin{aligned} D_{i,n}(n,k) &= (-1)^{n-1-i} \binom{n-1}{i} &\\ D_{i,n}(0,n) &= 1 &\text{($d = 0$)} \\ D_{i,n}(d,n-d) &= (-1)^{n-1-i} \binom{d-1}{i-(n-d)} &\text{if $d > 0$} \\ D_{i,n}(d-1,k+1) &= D_{i,n}(d-1,k) + D_{i,n}(d,k) \end{aligned}$

(19)

where as usual, 0 <= i < n and k >= 0.

Actually, if the binomial was correctly defined for negative values, the separation for d = 0 wouldn't have been necessary. According to me, the correct definition of a binomial of two negative values is $\binom{-1-y}{-1-x} = (-1)^{x-y}\binom{x}{y}$ , and thus, for d = 0, we have $(-1)^{n-1-i} \binom{d-1}{i-(n-d)} =$ $(-1)^{d-1-(i-(n-d))} \binom{d-1}{i-(n-d)} =$ $\binom{-1-(i-(n-d))}{-1-(d-1)} =$ $\binom{n-1-i}{0} = 1$ .

As an example, consider the following solution to D_3,8(d, k).

$\begin{array}{llllllllllll} 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 57 & 477 & 2277 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 56 & 420 & 1800 & 5775 \\ 0 & 0 & 1 & -1 & 0 & 0 & 0 & 56 & 364 & 1380 & 3975 & 9625 \\ 0 & 1 & -2 & 1 & 0 & 0 & 56 & 308 & 1016 & 2595 & 5650 & 11011 \\ 1 & -3 & 3 & -1 & 0 & 56 & 252 & 708 & 1579 & 3055 & 5361 & 8757 \\ -4 & 6 & -4 & 1 & 56 & 196 & 456 & 871 & 1476 & 2306 & 3396 & 4781 \\ 10 & -10 & 5 & 55 & 140 & 260 & 415 & 605 & 830 & 1090 & 1385 & 1715 \\ -20 & 15 & 50 & 85 & 120 & 155 & 190 & 225 & 260 & 295 & 330 & 365 \\ 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 \end{array}$

where k runs from left to right from 0 till 11, and d runs from top to bottom from 0 till n = 8. The top row is therefore P_3,8(k) and the first n+1 = 9 values equal H[k-1-i] = H[k-4]. The bottom row is D_3,8(8,k) = (-1)^n-1-i $\binom{n-1}{i}$ = (-1)^(8-1-3) $\binom{8-1}{3}$ = 35.

Since the last identity of (19) holds everywhere, it is actually easiest to generate D from the bottom line and the first column. The first column is

$\begin{split} D_{i,n}(d,0) &= \Delta^d [P_{i,n}](0) \\ &= \sum_{r=0}^d{(-1)^{d-r}\binom{d}{r}H[r-1-i]} \\ &= \sum_{r=i+1}^d{(-1)^{d-r}\binom{d}{r}} \\ &= \sum_{0}^{d-i-1}{(-1)^r\binom{d}{r}} \\ &= \begin{cases} 0 &\text{if $d = 0$} \\ (-1)^{d-i-1}\binom{d-1}{i} &\text{if $d > 0$} \\ \end{cases} \end{split}$

(20)

If binomial had been defined correctly for negative values, then the special case for d = 0 would not have been necessary. Unfortunately, it is. Therefore things are easier if we redefine D as

$\begin{aligned} &{P^1}_{i,n}(k) = \hat{P}_{i,n}(k) - 1 \\ &{D^1}_{i,n}(d,k) = \Delta^d[{P^1}_i,n](k) \end{aligned}$

(21)

This obviously has no influence on the values of D for d > 0, while the top row is simply reduced with 1.

$\begin{array}{llllllllllll} -1 & -1 & -1 & -1 & 0 & 0 & 0 & 0 & 0 & 56 & 476 & 2276 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 56 & 420 & 1800 & 5775 \\ 0 & 0 & 1 & -1 & 0 & 0 & 0 & 56 & 364 & 1380 & 3975 & 9625 \\ 0 & 1 & -2 & 1 & 0 & 0 & 56 & 308 & 1016 & 2595 & 5650 & 11011 \\ 1 & -3 & 3 & -1 & 0 & 56 & 252 & 708 & 1579 & 3055 & 5361 & 8757 \\ -4 & 6 & -4 & 1 & 56 & 196 & 456 & 871 & 1476 & 2306 & 3396 & 4781 \\ 10 & -10 & 5 & 55 & 140 & 260 & 415 & 605 & 830 & 1090 & 1385 & 1715 \\ -20 & 15 & 50 & 85 & 120 & 155 & 190 & 225 & 260 & 295 & 330 & 365 \\ 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 & 35 \end{array}$

It's not hard to see that this will make life a lot easier. The recurrence rules that generate D¹ do not have any special cases.

$\begin{aligned} {D^1}_{i,n}(n,k) &= (-1)^{n-1-i} \binom{n-1}{i} \\ {D^1}_{i,n}(d,0) &= (-1)^{d-i-1} \binom{d-1}{i} \\ {D^1}_{i,n}(d-1,k+1) &= {D^1}_{i,n}(d-1,k) + {D^1}_{i,n}(d,k) \end{aligned}$

(22)

It's not hard to construct D¹_i,n(d,k) from this. Each value in the left column gives an independent contribution that adds up to the rest. Consider a single 1 in the left column (with a row of zeroes below it). This would lead to:

$\begin{array}{llllllllllll} 0 & 0 & 0 & 0 & 1 & 5 & 15 & 35 & 70 & 126 & 210 & 330 \\ 0 & 0 & 0 & 1 & 4 & 10 & 20 & 35 & 56 & 84 & 120 & 165 \\ 0 & 0 & 1 & 3 & 6 & 10 & 15 & 21 & 28 & 36 & 45 & 55 \\ 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}$

from which we clearly see that a 1 in row j contributes $\binom{k}{j-d}$ to D¹_i,n(d,k). Moreover, since it's all addition, every additional 1 that is added to the same row in the first column gives the same contribution. Hence, a value x in row j contributes $x\binom{k}{j-d}$ to D¹_i,n(d,k). "Summing it all up" gives us the result

${D^1}_{i,n}(d,k) = \sum_{j=0}^n (-1)^{j-i-1}\binom{j-1}{i}\binom{k}{j-d}$

(23)

And thus we found that

$\begin{split} \hat{P}_{i,n}(k) &= 1 + {D^1}_{i,n}(0,k) \\ &= 1 + \sum_{j=0}^n (-1)^{j-i-1}\binom{j-1}{i}\binom{k}{j} \\ &= \sum_{j=1}^n (-1)^{j-i-1}\binom{j-1}{i}\binom{k}{j} \\ &= \sum_{j=0}^{n-1} (-1)^{j-i}\binom{j}{i}\binom{k}{j+1} \\ &= \sum_{j=i}^{n-1} (-1)^{j-i}\binom{j}{i}\binom{k}{j+1} \\ &= \sum_{j=0}^{n-1-i} (-1)^j\binom{j+i}{i}\binom{k}{j+i+1} \\ &= \sum_{j=0}^{n-1-i} (-1)^j\binom{j+i}{i}\binom{k}{-1-i-j+k} \\ &= \sum_{j=0}^{n-1-i} (-1)^j\binom{n}{j}\binom{n-1-i-j+k}{n} \\ &= P_{i,n}(k) \end{split}$

(24)

which proves that P_i,n(k) can be written as a polynomial in k of degree n. In fact, we can write it as a product of k and a polynomial of degree n-1 because P_i,n(0) = 0 for any i and n. Define

$P_{i,n}(k) = k/n! \sum_{s=0}^{n-1} c(s,i,n) k^s$

(25)

with coefficients c(s,i,n) that later will turn out to be integers (thanks to the wise choice of deviding by n! outside the sum).

Filling this in into (4c) gives

$\begin{split} R_{n,k}(u) &= k/n! \sum_{i=0}^{n-1} \sum_{s=0}^{n-1} c(s,i,n) k^s u^i \\ &= k/n! \sum_{s=0}^{n-1} \sum_{i=0}^{n-1} c(s,i,n) u^i k^s \\ &= k/n! \sum_{s=0}^{n-1} g(n,s,u) k^s \end{split}$

(26)

where

$g(n,s,u) = \sum_{i=0}^{n-1} c(s,i,n) u^i$

(27)

\[ \]

(1)

$x^{km}-1 = (x^m-1)^{n+1} \sum_{i=0}^{k-n-1}{\binom{k-1-i}{n}x^{mi}} + (x^m-1) \sum_{i=0}^{n-1}{P_{i,n}(k)x^{mi}}$

p devides x^m-1, thus pⁿ⁺¹ devides the first term. What remains is to prove that pⁿ devides the second sum. As was shown before, k devides $\sum_{i=0}^{n-1}{c_i P_{i,n}(k)}$ and thus the second sum, and pⁿ | k, so we are done.

The Pink Polynomials

I ran into these functions, basically by first finding the polynomials for n=1...6 given below and then discovering a structure in them. I named them "Pink" polynomials for an obvious reason. The 'P' stands for Polynomial.

The canonical definition of the Pink polynomial is that they are polynomials in the variable k, of degree n, defined for $0 \le i < n$ , where

$P_{i,n}(k) = \begin{cases} 0 & 0 \le k \le i \\ 1 & i < k \le n \\ \end{cases}$

(1)

Lemma 1

The polynomials can be constructed in the following "brute force" way,

$P_{i,n}(k) = \prod_{j=0}^i{(k-j)} \cdot \sum_{j=i+1}^n{\left((-1)^{(n+j)} \binom{n}{j} \prod_{z=i+1}^{j-1}{(k-z)} \prod_{l=j+1}^n{(k-l)}\right)} / n!$

(2)

where the first product takes care of the zeroes between 0 and i, while the sum takes care of the ones between i and n.

Proof

If 0 $\le$ k $\le$ i, then one of the factors of $\prod_{j=0}^i{(k-j)}$ is zero, and therefore (2) is zero, while if i < k $\le$ n, then each of the terms of the sum $\sum_{j=i+1}^n{\left((-1)^{(n+j)} \binom{n}{j} \prod_{z=i+1}^{j-1}{(k-z)} \prod_{l=j+1}^n{(k-l)}\right)}$ is zero except the one where j = k. Therefore (2) becomes k!/(k-(i+1))! (-1)^n+k n!/(k! (n-k)!) (k-(i+1))! (-1)^n-k (k-n)! /n! = 1. $\qed$

Examples

Here is a list of all Pink polynomials for n <= 6,

n=1
$P_{0,1}(k) = k$
n=2
$P_{0,2}(k) = k/2 \cdot (-k + 3)$
$P_{1,2}(k) = k/2 \cdot ( k - 1)$
n=3
$P_{0,3}(k) = k/6 \cdot ( k^2 - 6k + 11)$
$P_{1,3}(k) = k/6 \cdot (-2k^2 + 9k - 7)$
$P_{2,3}(k) = k/6 \cdot ( k^2 - 3k + 2)$
n=4
$P_{0,4}(k) = k/24 \cdot ( -k^3 + 10k^2 - 35k + 50)$
$P_{1,4}(k) = k/24 \cdot ( 3k^3 - 26k^2 + 69k - 46)$
$P_{2,4}(k) = k/24 \cdot (-3k^3 + 22k^2 - 45k + 26)$
$P_{3,4}(k) = k/24 \cdot ( k^3 - 6k^2 + 11k - 6)$
n=5
$P_{0,5}(k) = k/120 \cdot ( k^4 - 15k^3 + 85k^2 - 225k + 274)$
$P_{1,5}(k) = k/120 \cdot (-4k^4 + 55k^3 - 270k^2 + 545k - 326)$
$P_{2,5}(k) = k/120 \cdot ( 6k^4 - 75k^3 + 320k^2 - 525k + 274)$
$P_{3,5}(k) = k/120 \cdot (-4k^4 + 45k^3 - 170k^2 + 255k - 126)$
$P_{4,5}(k) = k/120 \cdot ( k^4 - 10k^3 + 35k^2 - 50k + 24)$
n=6
$P_{0,6}(k) = k/720 \cdot ( -k^5 + 21k^4 - 175k^3 + 735k^2 - 1624k + 1764)$
$P_{1,6}(k) = k/720 \cdot ( 5k^5 - 99k^4 + 755k^3 - 2745k^2 + 4640k - 2556)$
$P_{2,6}(k) = k/720 \cdot (-10k^5 + 186k^4 - 1300k^3 + 4170k^2 - 5890k + 2844)$
$P_{3,6}(k) = k/720 \cdot ( 10k^5 - 174k^4 + 1120k^3 - 3270k^2 + 4270k - 1956)$
$P_{4,6}(k) = k/720 \cdot ( -5k^5 + 81k^4 - 485k^3 + 1335k^2 - 1670k + 744)$
$P_{5,6}(k) = k/720 \cdot ( k^5 - 15k^4 + 85k^3 - 225k^2 + 274k - 120)$

Properties Of The Pink Polynomials

The Pink polynomials have the following properties.

$P_{i,n}(0) = 0$ , as follows directly from the definition (1). In other words, they all have k=0 as zero and thus k as factor.

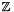The polynomials can be written as k/n! $\cdot$ Q(k) where Q(k) is a polynomial of degree n-1 over $\mathbb{Z}$ . This follows trivially from (2).

$Q_{i,n}(k) = \prod_{j=1}^i{(k-j)} \cdot \sum_{j=i+1}^n{\left((-1)^{(n+j)} \binom{n}{j} \prod_{z=i+1}^{j-1}{(k-z)} \prod_{l=j+1}^n{(k-l)}\right)}$

(3)

Since Q(k) is a polynomial of degree n-1, we should also be able to write this as,

$Q_{i,n}(k) = \sum_{s=0}^{n-1}{c_s(i,n) k^s}$

(4)

Where the c_s are the coefficients of the polynomial.

For $n,i \in \mathbb{Z}$ , define

$\eta(n,i) = \begin{cases} 0 & \text{if $n < 0$ or $i < 0$}\\ 1 & \text{if $n = 0$ and $i = 0$}\\ (n-1) \cdot \eta(n-1, i) + \eta(n-1, i-1) & \text{otherwise} \end{cases}$

(5a)

Since this function is my own invention, allow me to give a quick overview of some of it's characteristics,

$\begin{array}{lcll} \eta(0, 0) &=& 1 \\&&\\ \eta(0, i) &=& 0 & \text{for any $i \ne 0$} \\&&\\ \eta(n, 0) &=& 0 & \text{for any $n \ne 0$} \\&&\\ \eta(n, i) &=& 0 & \text{if $n < i$} \\&&\\ \eta(n, i) &>& 0 & \text{iff $i \ge 0$ and $n \ge i$} \\&&\\ \eta(n, 1) &=& (n-1)! & \text{if $n > 0$} \\&&\\ \eta(n, n) &=& 1 & \text{for any $n \ge 0$} \\&&\\ \sum_{i=0}^n {\eta(n, i)} &=& n! \\&&\\ \sum_{i=0}^{a}{\eta(n, i)} &=& n! - \sum_{i=0}^n {\eta(n, i+a+1)} \\&&\\ \sum_{i=0}^n {\eta(n,i) \binom{i}{s}} &=& \eta(n+1,s+1) \end{array}$

(5b)

P.S. It turns out that the $\eta$ are known as the unsigned Stirling numbers of the first kind: $\eta(n,i) = |s(n,i)| = (-1)^{n-i} s(n,i)$ .

It can be derived that

$\begin{array}{ll} \prod_{j=0}^{b}{(k - j)} = \sum_{j=0}^{b+1}{(-1)^{b+1-j} \eta(b+1, j) k^j} & \text{if $b \ge -1$} \end{array}$

(6)

from which we can conclude that for $b \ge a - 1$

$\begin{array}{lcl} \prod_{j=a}^{b}{(k - j)} &=& \prod_{j=0}^{b-a}{((k - a) - j)}\\&&\\ &=& \sum_{j=0}^{b-a+1}{(-1)^{b-a+1-j} \eta(b-a+1, j) (k-a)^j}\\&&\\ &=& \sum_{j=0}^{b-a+1}{\left((-1)^{b-a+1-j} \eta(b-a+1, j) \sum_{h=0}^j{(-1)^{j-h}\binom{j}{h}a^{j-h}k^h}\right)}\\&&\\ &=& \sum_{j=0}^{b-a+1}{ \sum_{h=0}^j{(-1)^{b-a+1-h}\eta(b-a+1, j)\binom{j}{h}a^{j-h}k^h}}\\&&\\ &=& \sum_{h=0}^{b-a+1}{ \sum_{j=h}^{b-a+1}{(-1)^{b-a+1-h}\eta(b-a+1, j)\binom{j}{h}a^{j-h}k^h}}\\&&\\ &=& \sum_{h=0}^{b-a+1}{\left((-1)^{b-a+1-h}\sum_{j=h}^{b-a+1}{\eta(b-a+1, j)\binom{j}{h}a^{j-h}}\right)k^h} \end{array}$

(7)

Hence, we can rewrite (3) as,

$\begin{array}{lcl} Q_{i,n}(k) &=& \left(\sum_{h=0}^i{\left((-1)^{i-h}\sum_{r=h}^i{\eta(i, r)\binom{r}{h}}\right)k^h}\right)\cdot\\&&\\ && \sum_{j=i+1}^n{\left\{(-1)^{(n+j)} \binom{n}{j}\left( \sum_{g=0}^{j-1-i}{\left((-1)^{j-1-i-g}\sum_{z=g}^{j-1-i}{\eta(j-1-i, z)\binom{z}{g}(i+1)^{z-g}}\right)k^g}\right) \sum_{f=0}^{n-j}{\left((-1)^{n-j-f}\sum_{l=f}^{n-j}{\eta(n-j, l)\binom{l}{f}(j+1)^{l-f}}\right)k^f}\right\}}\\&&\\ &=& \sum_{j=i+1}^n{\sum_{h=0}^i{\sum_{r=h}^i{\sum_{g=0}^{j-1-i}{\sum_{z=g}^{j-1-i}{\sum_{f=0}^{n-j}{\sum_{l=f}^{n-j} {(-1)^{j+h+g+f-1}\eta(i,r)\eta(j-1-i,z)\eta(n-j,l)\binom{r}{h}\binom{n}{j} \binom{z}{g}\binom{l}{f}(i+1)^{z-g}(j+1)^{l-f}k^{h+g+f}}}}}}}}\\&&\\ &=& \sum_{j=i+1}^n\sum_{h=0}^i\sum_{r=h}^i\sum_{g=0}^{j-1-i}\sum_{z=g}^{j-1-i}\sum_{s=h+g}^{n-j+h+g}\sum_{l=s-h-g}^{n-j} (-1)^{j+s-1}\eta(i,r)\eta(j-1-i,z)\eta(n-j,l)\binom{r}{h}\binom{n}{j} \binom{z}{g}\binom{l}{s-h-g}(i+1)^{z-g}(j+1)^{l-s+h+g}k^s\\&&\\ &=& \sum_{s=0}^{n-1}\sum_{j=i+1}^n\sum_{h=\max(0,s+i+1-n)}^{\min(s,i)}\sum_{r=h}^i\sum_{g=\max(0,s-h+j-n)}^{\min(j-1-i,s-h)}\sum_{z=g}^{j-1-i}\sum_{l=s-h-g}^{n-j} (-1)^{j+s-1}\eta(i,r)\eta(j-1-i,z)\eta(n-j,l)\binom{r}{h}\binom{n}{j} \binom{z}{g}\binom{l}{s-h-g}(i+1)^{z-g}(j+1)^{l-s+h+g}k^s\\&&\\ &=& \sum_{s=0}^{n-1}\sum_{j=i+1}^n\sum_{h=s+i+1-n}^s\sum_{r=h}^i\sum_{g=s-h+j-n}^{s-h}\sum_{z=g}^{j-1-i}\sum_{l=s-h-g}^{n-j} (-1)^{j+s-1}\eta(i,r)\eta(j-1-i,z)\eta(n-j,l)\binom{r}{h}\binom{n}{j} \binom{z}{g}\binom{l}{s-h-g}(i+1)^{z-g}(j+1)^{l-s+h+g}k^s \end{array}$

(8)

and thus found an expression of the $c_s(i,n)$ of (4),

$\begin{array}{lcl} c_s(i,n) &=& \sum_{j=i+1}^n\sum_{h=s+i+1-n}^s\sum_{r=h}^i\sum_{g=s-h+j-n}^{s-h}\sum_{z=g}^{j-1-i}\sum_{l=s-h-g}^{n-j} (-1)^{j+s-1}\eta(i,r)\eta(j-1-i,z)\eta(n-j,l)\binom{r}{h}\binom{n}{j}\binom{z}{g}\binom{l}{s-h-g}(i+1)^{z-g}(j+1)^{l-s+h+g}\\&&\\ &=& \sum_{j=i+1}^n\sum_{h=s+i+1-n}^s\sum_{r=h}^i\sum_{g=s-h+j-n}^{s-h}\sum_{z=g}^{j-1-i} (-1)^{n+h+g-1}\eta(i,r)\eta(j-1-i,z)\binom{r}{h}\binom{n}{j}\binom{z}{g}(i+1)^{z-g}(-1)^{n-j-s+h+g}\sum_{l=s-h-g}^{n-j}\eta(n-j,l)\binom{l}{s-h-g}(j+1)^{l-s+h+g}\\&&\\ &=& \sum_{j=i+1}^n\sum_{r=s+i+1-n}^i\sum_{h=s+i+1-n}^s\sum_{z=s-h+j-n}^{j-1-i}\sum_{g=s-h+j-n}^{s-h} (-1)^{n+h+g-1}\eta(i,r)\eta(j-1-i,z)\binom{r}{h}\binom{n}{j}\binom{z}{g}(i+1)^{z-g}(-1)^{n-j-s+h+g}\sum_{l=s-h-g}^{n-j}\eta(n-j,l)\binom{l}{s-h-g}(j+1)^{l-s+h+g}\\&&\\ &=& \sum_{j=i+1}^n\sum_{r=s+i+1-n}^i\sum_{z=j-n}^{j-1-i}\sum_{h=s-z+j-n}^s\sum_{g=s-h+j-n}^{s-h} (-1)^{n+h+g-1}\eta(i,r)\eta(j-1-i,z)\binom{r}{h}\binom{n}{j}\binom{z}{g}(i+1)^{z-g}(-1)^{n-j-s+h+g}\sum_{l=s-h-g}^{n-j}\eta(n-j,l)\binom{l}{s-h-g}(j+1)^{l-s+h+g}\\&&\\ &=& \sum_{j=i+1}^n\sum_{r=s+i+1-n}^i\sum_{z=j-n}^{j-1-i}\sum_{h=s-z+j-n}^s\sum_{f=0}^{n-j} (-1)^{n+s-f-1}\eta(i,r)\eta(j-1-i,z)\binom{r}{h}\binom{n}{j}\binom{z}{s-h-f}(i+1)^{z-s+h+f}(-1)^{n-j-f}\sum_{l=f}^{n-j}\eta(n-j,l)\binom{l}{f}(j+1)^{l-f}\\&&\\ \end{array}$

(9a)

Map j --> j+i+1, r --> r+s+i+1-n, l --> l+f then z --> z+j+i+1-n, then h --> h+s-z to get,

$\begin{array}{lcl} c_s(i,n) &=& \sum_{j=0}^{n-1-i}\sum_{r=0}^{n-1-s}\sum_{z=0}^{n-1-i}\sum_{h=0}^{z}\sum_{f=0}^{(n-1-i)-j}\sum_{l=0}^{((n-1-i)-j)-f} \\&&\\ && (-1)^{s+i+j}\eta(i,i-((n-1-s)-r))\eta(j,j-((n-1-i)-z))\eta((n-1-i)-j,l+f) \\&&\\ && \binom{s+r-(n-1-i)}{h+s-z}\binom{n}{j+i+1}\binom{z-((n-1-i)-j)}{z-h-f}\binom{l+f}{f}(i+1)^{h-(((n-1-i)-j)-f)}(j+i+2)^{l}\\&&\\ &=& \sum_{j=0}^{n-1-i} (-1)^{i+j} \binom{n}{j+i+1} \sum_{z=0}^{n-1-i} \eta(j,j-((n-1-i)-z)) \\&&\\ && \sum_{h=0}^{z} \sum_{f=0}^{(n-1-i)-j} \binom{z-((n-1-i)-j)}{z-h-f} (i+1)^{h-(((n-1-i)-j)-f)} \\&&\\ && \sum_{l=0}^{((n-1-i)-j)-f} \eta((n-1-i)-j,l+f) \binom{l+f}{f} (j+i+2)^{l} \\&&\\ && \sum_{r=0}^{n-1-s} (-1)^s \eta(i,i-((n-1-s)-r)) \binom{i-((n-1-s)-r)}{s-(z-h)} \end{array}$

(9b)

We might as well start the sum over f from ((n-1-i)-j)-h because for smaller f, z-h-f > z-((n-1-i)-j) and the subsequent binomial is zero anyway. Map f --> f+((n-1-i)-j)-h to get something that starts at 0 again and we have,

$\begin{array}{lcl} c_s(i,n) &=& \sum_{j=0}^{n-1-i} (-1)^{(n-1-i)-j} \binom{n}{(n-1-i)-j} \sum_{z=0}^{n-1-i} \eta(j,j-((n-1-i)-z)) \\&&\\ && \sum_{h=0}^z \sum_{f=0}^h \binom{z-((n-1-i)-j)}{z-((n-1-i)-j)-f} (n-(n-1-i))^f \\&&\\ && \sum_{l=0}^{h-f} \eta((n-1-i)-j,((n-1-i)-j)-(h-f)+l) \binom{((n-1-i)-j)-(h-f)+l}{((n-1-i)-j)-(h-f)} (n+1-((n-1-i)-j))^{l} \\&&\\ && \sum_{r=0}^{n-1-s} (-1)^{n-1-s} \eta(i,i-((n-1-s)-r)) \binom{i-((n-1-s)-r)}{s-(z-h)} \end{array}$

(9c)

Apparently it makes more sense to number i and s the other way around. Let $\hat{\imath} = n-1-i$ , $\hat{s} = n-1-s$ . Also inverse j and r, and replace some $\binom{n}{m}$ binomials with $\binom{n}{n-m}$ .

$\begin{array}{lcl} c_{\hat{s}}(\hat{\imath},n) &=& \sum_{j=0}^{\hat{\imath}} (-1)^j \binom{n}{j} \sum_{z=0}^{\hat{\imath}} \eta(\hat{\imath}-j,\hat{\imath}-j-(\hat{\imath}-z)) \\&&\\ && \sum_{h=0}^z \sum_{r=0}^{\hat{s}} (-1)^{\hat{s}} \eta(n-1-\hat{\imath},n-1-\hat{\imath}-r) \binom{n-1-\hat{\imath}-r}{n-1-\hat{s}-(z-h)} \\&&\\ && \sum_{f=0}^h \binom{z-j}{f} (n-\hat{\imath})^f \\&&\\ && \sum_{l=0}^{h-f} \eta(j,j-(h-f)+l) \binom{j-(h-f)+l}{l} (n+1-j)^l \\&&\\ &=& \sum_{j=0}^{\hat{\imath}} (-1)^j \binom{n}{j} \sum_{z=j}^{\hat{\imath}} \eta(\hat{\imath}-j,\hat{\imath}-j-(\hat{\imath}-z)) \\&&\\ && \sum_{h=0}^z \sum_{r=0}^{n-1-\hat{\imath}} (-1)^{\hat{s}} \eta(n-1-\hat{\imath},n-1-\hat{\imath}-r) \binom{n-1-\hat{\imath}-r}{n-1-\hat{s}-(z-h)} \\&&\\ && \sum_{f=0}^h \binom{z-j}{f} (n-\hat{\imath})^f \\&&\\ && \sum_{l=h-f-j}^{h-f} \eta(j,j-(h-f)+l) \binom{j-(h-f)+l}{l} (n+1-j)^l \end{array}$

(9d)

where the last (actually, non trivial) transformation makes sure that $\eta$ is never called with negative arguments. Nevertheless, now it is apparent that we can simplify this even more by also inverting r (relative to $n-1-\hat{\imath}$ ). This then gives

$\begin{array}{lcl} c_{\hat{s}}(\hat{\imath},n) &=& \sum_{j=0}^{\hat{\imath}} (-1)^j \binom{n}{j} \sum_{z=j}^{\hat{\imath}} \eta(\hat{\imath}-j,\hat{\imath}-j-(\hat{\imath}-z)) \\&&\\ && \sum_{h=0}^z \sum_{r=0}^{n-1-\hat{\imath}} (-1)^{\hat{s}} \eta(n-1-\hat{\imath},r) \binom{r}{n-1-\hat{s}-(z-h)} \\&&\\ && \sum_{f=0}^h \binom{z-j}{f} (n-\hat{\imath})^f \\&&\\ && \sum_{l=h-f-j}^{h-f} \eta(j,j-(h-f)+l) \binom{j-(h-f)+l}{l} (n+1-j)^l \end{array}$

(9e)

Filling in k = 0 in (7), and replacing a with -a gives the relationship:

$\begin{array}{lcl} \prod_{j=-a}^{b}{(-j)} &=& \sum_{h=0}^{a+b+1}{ \sum_{j=h}^{a+b+1}{(-1)^{a+b+1-h}\eta(a+b+1, j)\binom{j}{h}(-a)^{j-h}0^h}}\\&&\\ &=& \sum_{j=0}^{a+b+1}{(-1)^{a+b+1-j}\eta(a+b+1, j) a^{j}} \end{array}$

(10)

Lemma 2

The sum over i of the constant term of each Pink function, $\sum_{i=0}^{n-1}{Q_{i,n}(0)}$ , equals n factorial.

Proof

$\begin{array}{lcl} \sum_{i=0}^{n-1}{Q_{i,n}(0)} &=& \sum_{i=0}^{n-1}{\left((-1)^i\prod_{j=1}^i{j} \cdot \sum_{j=i+1}^n{\left((-1)^{n+j}\binom{n}{j}(-1)^{j-1-i}\prod_{z=i+1}^{j-1}{z} \cdot (-1)^{n-j} \prod_{l=j+1}^n{l}\right)}\right)}\\&&\\ &=& \sum_{i=0}^{n-1}{\left(i! \sum_{j=i+1}^n{\left((-1)^{j-1} \cdot n!/(j!\ (n-j)!) \cdot (j-1)!/i! \cdot n!/j!\right)}\right)}\\&&\\ &=& (n!)^2 \sum_{i=0}^{n-1}{\sum_{j=i+1}^n{\left((-1)^{j-1}/(j!\ (n-j)! j)\right)}}\\&&\\ &=& (n!)^2 \sum_{j=1}^n{\sum_{i=0}^{j-1}{\left((-1)^{j-1}/(j!\ (n-j)! j)\right)}}\\&&\\ &=& (n!)^2 \sum_{j=1}^n{\left((-1)^{j-1}/(j!\ (n-j)!)\right)}\\&&\\ &=& n! \left(\sum_{j=0}^n{\left((-1)^{j-1}\binom{n}{j}\right)} - \left((-1)^{0-1}\binom{n}{0}\right)\right)\\&&\\ &=& n! \end{array}$