libecc: Elliptic Curve Cryptography C++ Library

Main Page Reference Manual Compound List File List

Elementary Symmetrical Polynomials

The elementary symmetrical polynomials (ESP's) are polynomials in n indeterminates that are symmetrical, that is, they don't change under the permuation of the indeterminates.

They are defined as follows.

S₁(t₁, t₂, 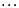$\cdots$ , t_n) = t₁ + t₂ + 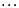$\cdots$ + t_n
S₂(t₁, t₂, 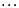$\cdots$ , t_n) = t₁t₂ + t₁t₃ + 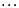$\cdots$ + t₁t_n + t₂t₃ + t₂t₄ + 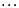$\cdots$ + t₂t_n + t₃t₄ + 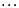$\cdots$ + t_n-1t_n
S₃(t₁, t₂, 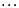$\cdots$ , t_n) = t₁t₂t₃ + t₁t₂t₄ + 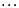$\cdots$ + t₁t₂t_n + 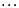$\cdots$ + t₁t_n-1t_n + 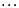$\cdots$ + t_n-2t_n-1t_n
$\vdots$
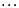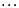S_n(t₁, t₂, $\cdots$ , t_n) = t₁t₂ $\cdots$ t_n

In other words, S_k exists of a sum of all permutations of products of precisely k different t_j. There are 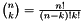$\binom{n}{k} = \frac{n!}{(n-k)!k!}$ such permutations for a given n and k.

A more formal way of defining the ESP's is

$S_k(t_1, t_2, \ldots, t_n) = \sum_{1 \leq i_1 < i_2 < \cdots < i_k \leq n}{t_{i_1}t_{i_2} \cdots t_{i_k}}$

Newton Symmetrical Polynomials

The Newton Symmetric Polynomials (NSP's) on (t₁ t₂ 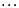$\cdots$ t_n) are the polynomials

$N_k(t_1, t_2, \ldots, t_n) = \sum_{i=1}^n{t_i^k}$

Newton and Elementary Symmetrical Polynomials

For a fixed n, the set { S₁, S₂, ..., S_n } is linearly independend; they cannot be expressed into eachother. Since there are n indeterminates and n elementary symmetric polynomials, they form a basis for the set of symmetric polynomials of n indeterminates. The same holds for the set { N₁, N₂, ..., N_n }. Every symmetric polynomial can be expressed as a polynomial of the ESP's or NSP's, in particular they can be expressed into eachother.

A recursive formula that expresses one into the other still looks reasonably simple. Therefore this is the prefered way. For a fixed n the relationship is given by

$S_k = \frac{1}{k}(S_{k-1}N_1 - S_{k-2}N_2 + \ldots \pm S_1N_{k-1} \mp N_k)$

from which it is easy to derive the reverse relationship

$N_k = S_1N_{k-1} - S_2N_{k-2} + \ldots \pm S_{k-1}N_1 \mp kS_k$

Both cases exist of a sum with k - 1 leading terms, followed by the last term. In particular, N₁ = S₁.

Symmetric polynomials

Elementary Symmetrical Polynomials

Newton Symmetrical Polynomials

Newton and Elementary Symmetrical Polynomials