libecc: Elliptic Curve Cryptography C++ Library

Main Page Reference Manual Compound List File List

Introduction

As was deduced from the brute force point counting data for all possible elliptic curves of the form x³ + ax² + b = y² + xy over binary fields up till and including extension degree m = 10, the values of parameter a can be devided into two sets, both of a size q/2, where q = 2^m is the cardinality of the field and therefore equal to the number of possible values of a. 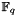Let us call these two sets A₀ and A₁ so that A₀ $\cup$ A₁ = $\mathbb{F}_q$ , A₀ $\cap$ A₁ = $\emptyset$ and A₀ = A₁ = q/2.

Then furthermore it was found that A₀ and A₁ are only a function of the field (GF(2^m)/<t^m+t^k+1>) and not of b. Let a₀ $\in$ A₀ and a₁ $\in$ A₁, and then define the curves E₀ and E₁ to be E₀: x³ + a₀x² + b = y² + xy and E₁: x³ + a₁x² + b = y² + xy, then it was found that for some fixed b also #E₀ and #E₁ are fixed (not depending on the specific choice of a₀ and a₁ respectively) and that #E₀ + #E₁ = 2(q + 1). (Note: the notation #E is often used in literature to denote the cardinality of the Abelian group formed by the points of the elliptic curve E).

We would like to find how A₀ and A₁ depend on the field parameters, because that will reduce the amount of computations needed during the continuation of this research dramatically, as then we only have to try two values of a instead of q values.

A hyperplane

The finite field $\mathbb{F}_{2^m}$ , called a binary field, can be viewed as a vector space of dimension m over $\mathbb{F}$ ₂. That is, there exists a set of m elements { $\alpha$ ₀, $\alpha$ ₁, ..., $\alpha$ _m-1} in $\mathbb{F}_{2^m}$ such that each a $\in$ $\mathbb{F}_{2^m}$ can be written uniquely in the form

$a = \sum_{i=0}^{m-1} c_i\alpha_i$

where c_i $\in$ {0,1}.

The set { $\alpha$ ₀, $\alpha$ ₁, ..., $\alpha$ _m-1} is called a basis of $\mathbb{F}_{2^m}$ over $\mathbb{F}$ ₂. We can then represent a as a binary vector (c₀, c₁, ..., c_m-1). Libecc uses the polynomial basis, so in our case we just have $\alpha$ _i = tⁱ where t is the fixed complex (or whatever) root of our reduction trinomial t^m + t^k + 1. (Note that it is possible to chose another basis, called a normal basis, of the form { $\beta$ , $\beta$ ², $\beta$ ^2², ..., $\beta$ ^{2^m-1}} where $\beta$ $\in$ $\mathbb{F}_{2^m}$ . It is well known that such a basis always exists).

The observation that A₀ is exactly half of the total space, and considering that there are only two possible values per 'dimension', indicates that A₀ is a subspace of $\mathbb{F}_{2^m}$ of one dimension less than $\mathbb{F}_{2^m}$ .

It seems highly unlikely that this subspace would be 'curved'. I cannot prove this at this point, but it seems to me that there must be some kind of symmetry between the different dimensions: when we exchange any two coordinates then there shouldn't be a dramatic impact on the other coordinates. One property of a given coordinate c_i that I expect to stay fixed under the permutation of the other coordinates is the property of whether or not toggling c_i causes us to switch between A₀ and A₁. This doesn't mean that a permutation of the other coordinates doesn't cause us to switch between A₀ and A₁ too, but it shouldn't cause us to change from switching to non-switching.

HYPOTHESIS 1

A₀ is a hyperplane.

As one of the goals of this project is to reach people who did not study mathematics, lets first explain what a hyperplane means. Consider some n-dimensional vector space for which there exists an orthogonal basis. An orthogonal basis is a basis of elements (vectors) of that vector space that are all orthogonal to eachother. Orthogonal means, in terms of vectors, that they make an angle of 90 degrees with eachother. When two vectors are orthogonal, then their inproduct will be zero. I hestitate to explain inproduct, because when you don't know that then I doubt you would be reading this in the first place. But why not, the inproduct of two vectors can be calculated by multiplying their coordinates pair-wise and then summing up all those products. Thus, if one vector has coordinates (1,1,0,0,1,0,1) (in some seven dimensional space) and another one has coordinates (0,0,1,1,0,1,0) then they make an angle of 90 degrees because 1*0 + 1*0 + 0*1 + 0*1 + 1*0 + 0*1 + 1*0 = 0. A hyperplane is a subspace of one dimension less than the space in which it is contained (mathematicians would say, of codimension 1) that is 'flat'. That means that there exists a fixed vector n that that is a normal of the hyperplane at any point (it makes an angle of 90 degrees with the hyperplane at any point; or in other words with any vector that is the result of subtracting two arbitrary, though distinct, vectors that are element of the hyperplane). Ok, by now you should get the picture that the thing is 'flat'!

Let us next show that a hyperplane indeed fulfills the intuitive feeling that whether or not toggling any bit of a causes us to either switch between A₀ and A₁ or not, independent of the choice of the other bits. Lets use the notation from above and write a as a binary vector (c₀, c₁, ..., c_m-1) where c_i $\in$ {0,1} represents the bits of a. Furthermore, let n be represented by the binary vector (n₀, n₁, ..., n_m-1). Without loss of generality, we can chose a = 0 = (0, 0, ..., 0) to be element of A₀ (it has to be an element of either A₀ or A₁, so why not A₀). Assume that A₀ is a hyperplane and that n is the normal of that hyperplane. Then the angle that the vector n makes at any point a₀ $\in$ A₀ will be 90 degrees, as per our definition that n is the normal of the hyperplane A₀. And that means that the inproduct of n with a₀ - a_i will be 0 for any arbitrary a_i $\in$ A₀. Therefore also for a_i = 0. Let (a_0,0, a_0,1, ..., a_0,m-1) be the vector representation of a₀ then the inproduct can be written as $\sum_{i=0}^{i=m-1}n_ia_{0,i} = 0$ [mod 2]. And since the n_i are fixed, this clearly shows that when n_i = 0 then changing a_0,i has no influence on the result of the inproduct and therefore will not cause a change of a₀ being an element of A₀. While when n_i = 1 then changing the corresponding bit a_0,i will toggle the outcome of the inproduct and hence cause that vector not to be an element of A₀ anymore. And this is independent of the value of any of the other bits.

Understanding the above (and still assuming that A₀ is indeed a hyperplane of course) it is very easy to find the normal (n₀, n₁, ..., n_m-1). One only has to try each value of a with exactly one bit set (which are only m different values). Let this single bit be c_j so that

$c_i = \begin{cases} 0 & i \neq j \\ 1 & i = j \end{cases}$

If, using this a, the resulting curve has the cardinality #E₀, the cardinality corresponding to A₀, then the inproduct has to be 0 (because we defined that a = 0 is element of A₀). The inproduct will therefore have to equal 1 precisely for each j that corresponds to A₁ and thus has a cardinality #E₁ 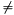$\neq$ #E₀! And the inproduct will only be 1 when n_j = 1.

An algorithm for finding the normal n of hyperplane A₀ could therefore be the following:

Find the cardinality of the curve with a = 0 and some fixed b (#E₀).
Find the cardinality of all curves with a parameter a that has exactly one bit set, c_j, using the same fixed parameter b.
If the cardinality of the curve with just c_j set is equal to #E₀ then n_j = 0, otherwise n_j = 1.

There is a little problem with this algorithm. This project has two goals: 1) to make elliptic curve cryptography more accessible to people without a mathematic university degree, and 2) to be the first Open Source project providing the means to generate your own cryptographically safe curves, which basically comes down to providing the means to determine the cardinality of an arbitrary elliptic curve. Therefore, an algorithm with the phrase "Find the cardinality of all curves ... blah blah" is easier said than done. Surely, we can do the above brute force, and it would be feasible for curves over fields up till extension degrees of m = 31, and that might be enough to guess a relationship between A₀ and m, but... we still have a hypothesis to prove too, namely that A₀ is indeed a hyperplane and using the above algorithm won't prove that at all, it will just give results. Therefore, it would be necessary to check in addition whether or not the resulting normal n is indeed a normal to all a₀ $\in$ A₀! And determining the cardinality of the curves for any a is really too much and/or will not give enough data points to feel secure about the hypothesis...

Time to become really smart therefore (and believe it or not but I am actually proud of the following, heheh).

Suppose for a moment that #E₀ is a multiple of 4 (as is the case as I will show below). That is, #E₀ = 4k for some k $\in$ $\mathbb{N}$ . Then #E₁ = 2(q + 1) - #E₀ = 2(2^m + 1) - 4k $\equiv$ 2 mod 4 for m $\geq$ 1. In other words, then #E₁ is not divisable by 4.

Further, recall that the order of any point on the curve devides the cardinality of the curve. That means that if we can find any point that has order 4, then the curve must have a cardinality that is divisable by 4. Moreover, we are free to chose any arbitrary value of b for this investigation (as A₀ does not depend on it). So, we can chose b = 1.

Then it is easy to prove that there is always a solution to the curve with a = 0 with x coordinate 1. Recall that E₀: x³ + a₀x² + b = y² + xy and set a₀ = 0, b = 1 and x = 1 to get 0 = y² + y, which has two solutions y = 0 and y = 1. And thus, the point P = (1, 0) is an element of this curve. Now lets calculate the order of P. Doubling the point, using the known rules,

Doubling a point P

If P_x = 0, then 2P = 0.

Provided that P_x is not 0,

2P = R where

s = P_x + P_y / P_x

R_x = s² + s + a and R_y = P_x² + (s + 1)R_x

gives us the following for our P = (1, 0). s = 1 + 0 / 1 = 1, R_x = 1 + 1 + 0 = 0 and R_y = 1 + (1 + 1)0 = 1. In other words 2P = (0, 1). And because now the x coordinate is 0, doubling this point again results in 0 (the "point at infinity"). So, the order of this point is 4 independent of the extension degree of the field (we only used that the field characteristic is 2)!

This in turn means that the cardinality of every elliptic curve of the form E₀¹: x³ + a₀x² + 1 = y² + xy over $\mathbb{F}_{2^m}$ , with a₀ $\in$ A₀ is a multiple of 4, for any m. Conversely, also for any m, every elliptic curve of the form E₁¹: x³ + a₁x² + 1 = y² + xy over $\mathbb{F}_{2^m}$ , with a₁ $\in$ A₁ is not divisable by 4, as was shown above.

As we saw before, there will always be a solution to the general elliptic equation E: x³ + ax² + b = y² + xy. for which x 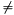$\neq$ 0, let us call those solutions (x, y) for now and remember that x 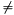$\neq$ 0. But there does not necessarily exist a solution with x = $\sqrt[4]{b}$ (huh, where did that come from? Well, that will become clear in a minute).

Please note that the only solution to x⁴ = b is the unique x = $\sqrt[4]{b}$ , because as we saw before there is only a single solution for a square root in a field with characteristic 2, and likewise there is only a single solution for $\sqrt[4]{b} = \sqrt{\sqrt{b}}$ .

Consider the equation

x³ + ax² + x⁴ = y² + xy

This equation can only ever be true when x = $\sqrt[4]{b}$ , because x and y are given to satisfy the curve equation and thus the above equation is equivalent with x⁴ = b (just add the curve equation to it).

We can rewrite this equation as x⁴ + y² + x³ + xy + ax² = 0 and then, remembering that x 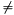$\neq$ 0, divide both sides by x² to get

x² + y²/x² + x + y/x + a = 0

Because of the field characteristic 2, we have x² + y²/x² = (x + y/x)². Then, with s = x + y/x, the equation becomes equivalent with

s² + s + a = 0

Now looking again to the rules for point doubling, this means that adding (x, y) to itself will result in a point with x-coordinate 0, if and only if x = $\sqrt[4]{b}$ ! In other words, when ( $\sqrt[4]{b}$ , y ) is a solution of the elliptive curve then this point will have order 4 and the cardinality of the curve will be a multiple of 4 and the chosen parameter a must be element of A₀. However, if there is no solution with x = $\sqrt[4]{b}$ then there exists no point with order 4, and thus 4 does not devide the cardinality of the curve and the chosen parameter a must be element of A₁.

This result did not use my hypothesis that A₀ is a hyperplane, but it also doesn't give us a formula for A₀. We'd still have to try every possible value of a, but at least we don't have to calculate a cardinality anymore!

Assuming that A₀ is a hyperplane however, we can now formulate the much faster algorithm (using x = b = 1, and using the fact that a with just bit c_j set is equal to t^j):

Try to solve the equation y² + y + t^j = 0, where j runs over all bits of a, 0 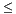$\leq$ j < m.
If there is a solution then n_j = 0, otherwise n_j = 1.

This algorithm is fast enough for every m and will suffice to find two values of a that do not result in two isomorphic curves. Since we can always use a = 0 for E₀ it will even suffice to find just a single j for which the above equation is not soluble.

If A₀ is not (always) a hyperplane then in order to find all of A₀ we'd have find all a₀ for which there exists a solution for y² + y + a₀ = 0. Also in this case it will suffice to find just a single a₁ for which the equation is not soluble, but - it might come in handy later when we actually known what A₀ is, and therefore I'd like to prove that it is, in fact, a hyperplane.

In order to do that we need two new mathematical tools. The Frobenius automorphism and the trace. I dedicated a special chapter to each, so please follow those links and get yourself familiar with these expressions.

PROOF OF HYPOTHESIS 1

Ok, now we have the mathematical tools to actually prove that A₀ is a hyperplane.

Recall that A₀ exists of all elements a₀ for which there exists a y such that y² + y + a₀ = 0. Then, using theorem 5, we can immediately conclude that those are the values for which the trace is 0. And thus

$\begin{matrix} Tr(a_0) = 0 \\ Tr(a_1) = 1 \end{matrix}$

Let t^j be an element of A₁, so that Tr(t^j) = 1, then it is now easy to see that toggling that bit will switch between A₀ and A₁ independent of the value of the other bits:

$Tr(a + t^j) = Tr(a) + Tr(t^j) = Tr(a) + 1$

And that proves that A₀ (and A₁) is a hyperplane.

Our quest continues in the next chapter Cracking parameter b of the elliptic curve .

Cracking parameter a of the elliptic curve

Introduction

A hyperplane

PROOF OF HYPOTHESIS 1