Theory: The trace of a field element
You probably already heard of the trace of a matrix. It is defined as the sum of the diagonal elements of a square matrix. What is so special about that? Well, as explained by that link, the trace is basis invariant. Let L : K be a finite field extension, like  is a field extension of
is a field extension of 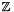 2. Given some linear transformation A: L
2. Given some linear transformation A: L  L you can write that linear transformation in the form of a matrix equation (because it is linear)
L you can write that linear transformation in the form of a matrix equation (because it is linear)  after chosing some basis for L that associates L with a vector space. This equation is linear in x because y is fixed. We already saw discussed one such basis for our field
after chosing some basis for L that associates L with a vector space. This equation is linear in x because y is fixed. We already saw discussed one such basis for our field  , elsewhere: (1, t, t2, t3, ..., tm-1).
, elsewhere: (1, t, t2, t3, ..., tm-1).
Lets work out a simple example using this polynomial basis. Let m = 4, using reduction polynomial t4 + t + 1. Let y = t, some element of our field  24. The linear transformation that sends x
24. The linear transformation that sends x  yx is then given by, Atx = tx. The trace of the matrix should be independent of the chosen basis, so that we might as well talk about "the trace of the linear transformation", or even about "the trace of y", for y uniquely determines this transformation. Multiplying with t means that this transformation sends 1 to t, t to t2, ... and tm-2 to tm-1. Only the transformation of the last member of our polynomial basis is a little different: tm-1
yx is then given by, Atx = tx. The trace of the matrix should be independent of the chosen basis, so that we might as well talk about "the trace of the linear transformation", or even about "the trace of y", for y uniquely determines this transformation. Multiplying with t means that this transformation sends 1 to t, t to t2, ... and tm-2 to tm-1. Only the transformation of the last member of our polynomial basis is a little different: tm-1  ttm-1 = tk + 1. Writing out the matrix for the given example gives therefore,
ttm-1 = tk + 1. Writing out the matrix for the given example gives therefore,
![\[ \begin{pmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} = t \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} \]](form_1022_279.png)
where xi is the coefficient corresponding to the basis element ti.
We find that in this case the trace is Tr(At) = Tr(t) = 0 (the sum of the diagonal elements of the matrix). Please note that Tr(y) is an element of K (being 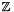 2 in our case): adding the diagonal elements (which are all element of K) is still done modulo 2!
2 in our case): adding the diagonal elements (which are all element of K) is still done modulo 2!
The more general matrix (for arbitrary m for which there exists an irreducible trinomial tm + tk + 1 that is used as reduction polynomial) leads to the matrix
![\[ \begin{pmatrix} 0 & 0 & 0 & \cdots & & & & \cdots & 0 & 1 \\ 1 & 0 & & & & & & & & 0 \\ 0 & 1 & 0 & & & & & & & 0 \\ 0 & & 1 & 0 & & & & & & \vdots \\ \vdots & & & \ddots & \ddots & & & & & 0 \\ & & & & 1 & 0 & & & & 1 \\ & & & & & 1 & 0 & & & 0 \\ \vdots & & & & & & \ddots & \ddots & & \vdots \\ 0 & & & & & & & 1 & 0 & 0 \\ 0 & \cdots & & & & & \cdots & 0 & 1 & 0 \end{pmatrix} \]](form_1022_280.png)
where the lower 1 in the right-most column appears in the k-th row, and hence we can immediately see that
![\[ Tr(t) = \begin{cases} 0 & k \neq m - 1 \\ 1 & k = m - 1 \end{cases} \]](form_1022_281.png)
Since libecc forbids values of k > m/2, we can safely assume that in our case the trace of t is always 0.
Lets investigate that this trace is indeed independent of the chosen basis by applying a basis transformation. The only possible basis transformation happens to be applying Frobenius a number of times. Lets investigate applying Frobenius once.
The Frobenius map sends 1  1, t
1, t  t2, t2
t2, t2  t4 = t + 1 and t3
t4 = t + 1 and t3  t6 = t3 + t2. From which follows that the corresponding matrix is
t6 = t3 + t2. From which follows that the corresponding matrix is
![\[ Frob(x) = \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} \]](form_1022_282.png)
the inverse of which is
![\[ Frob^{-1}(z) = \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} = \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} \]](form_1022_283.png)
Applying Frobenius to the equation Atx = tx gives Frob(Atx) = Frob(tx) = t Frob(x), where the last equality holds because that t is a constant. Furthermore, Frob(Atx) = Frob(At Frob-1(Frob(x))) = Frob(At Frob-1(z)), which brings us to the matrix equation
![\[ \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} = t \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} \]](form_1022_284.png)
Working out the matrix multiplication we get
![\[ \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} = t \begin{pmatrix} z_0 \\ z_1 \\ z_2 \\ z_3 \end{pmatrix} \]](form_1022_285.png)
where the zi are the coefficients relative to the basis (1, t2, t + 1, t3 + t2). And indeed, still we have Tr(t) = 1 + 1 + 1 + 1 = 0.
More in general, any change of basis can be represented with some non-singular matrix (which means that its determinant is non-zero and thus that it has an inverse). Let the matrix B represent a change of basis, then the matrix At will change into BAt/B, preserving the value of the determinant (see formula 18 on this page) and the value of the trace (see formula 7 on this page).
The following is not a proof in any way, but it gives things a bit a place, and therefore making it easier to understand more mathematical texts that actually derive and prove things, I hope.
Consider the linear equation (using some basis)
![\[ (A_i - \lambda_iI)x_i = 0 \]](form_1022_286.png)
Then  i are the eigen values of A and xi are the corresponding eigen vectors. Note that for a fixed
i are the eigen values of A and xi are the corresponding eigen vectors. Note that for a fixed  i the above represents the linear transformation (Aixi =
i the above represents the linear transformation (Aixi =  ixi).
ixi).
For the story about eigen values and corresponding eigen vectors,  i has to be an element of the base field K (
i has to be an element of the base field K (  2), so we really only have one non-trivial eigen value: 1. Plugging that value into the equation turns A into the identity matrix and trivally all of the vector space into the corresponding eigen space (that is, every value of x is an eigen vector of the identity matrix with scaling factor 1; what else is new). But we can also consider values for y =
2), so we really only have one non-trivial eigen value: 1. Plugging that value into the equation turns A into the identity matrix and trivally all of the vector space into the corresponding eigen space (that is, every value of x is an eigen vector of the identity matrix with scaling factor 1; what else is new). But we can also consider values for y =  i that are element of L, in that case we simply get the equation Ayx = yx which holds per definition for any value x
i that are element of L, in that case we simply get the equation Ayx = yx which holds per definition for any value x  L. Nevertheless, we can still call y eigen value and related theorems still hold, like that the trace of the matrix is the sum of all its eigen values (now elements of L), and the norm of the matrix (its determinant) is the product of all the eigen values. Below we assume that the eigen values y
L. Nevertheless, we can still call y eigen value and related theorems still hold, like that the trace of the matrix is the sum of all its eigen values (now elements of L), and the norm of the matrix (its determinant) is the product of all the eigen values. Below we assume that the eigen values y  L and you can forget about the concept of eigen vectors: the equations are trivially true for any x. This paragraph was just added to take away possible confusion about that.
L and you can forget about the concept of eigen vectors: the equations are trivially true for any x. This paragraph was just added to take away possible confusion about that.
Obviously (Ay - yI) can't have an inverse when (Ay - yI)x = 0 for every x 
 . The matrix will be singular therefore, its determinant will be zero and we have = 0. The determinant is a polynomial in y of degree m and the equation is called the characteristic equation (or polynomial) of Ay; the roots are the eigen values of the matrix.
. The matrix will be singular therefore, its determinant will be zero and we have = 0. The determinant is a polynomial in y of degree m and the equation is called the characteristic equation (or polynomial) of Ay; the roots are the eigen values of the matrix.
If we choose y = t and consider
![\[ A_tx = tx \]](form_1022_288.png)
or
![\[ (A_t - tI)x = 0 \]](form_1022_289.png)
then the equation = 0 must be the minimal polynomial of t (that is, a monomial of degree m): it is the reduction polynomial! The corresponding At will have eigen values that are precisely the roots of the reduction polynomial. What are those roots?
We already have one root (per definition): t itself. It is near impossible to write out t in its complex form, that would result in huge formulas if at all possible to find, but we don't have to do that. We can express the other roots easily in t by repeatedly applying Frobenius.
For example, let the reduction polynomial be t4 + t + 1 = 0. Then by replacing each t with its square, the equation still holds: (t2)4 + t2 + 1 = t4t4 + t2 + 1 = (t + 1)2 + t2 + 1 = t2 + 1 + t2 + 1 = 0. And doing that again, it still holds: (t4)4 + t4 + 1 = (t + 1)4 + t4 + 1 = 0, and so on. After all, the Frobenius map is an automorphism. If t is a generator of the field and its order is n = 2m - 1, hence n is the smallest positive integer such that tn = 1, then applying Frobenius m - 1 times will lead necessarily to m different values. The roots of the reduction polynomial are therefore given by the set (t, t2, t22, ..., t2m-1) and they represent the eigen values of the matrix At in the linear transformation Atx = tx, independent of the basis. If t is not a generator of the field, which is possible when m is non-prime, it might happen that the same eigen value is shared by more than one eigen vector, but in that case we have to add the same eigen value multiple times. Therefore, the trace of t is given by the sum of this set and the det is given by the product of this set.
The same story holds for an arbitrary value of y (not zero), and we find
![\[ Tr(y) = \sum_{i=0}^{m-1}{y^{2^i}} \]](form_1022_290.png)
Also note that  which makes us jump of joy because it means that every non-zero y has an inverse, as should be the case for field elements!
which makes us jump of joy because it means that every non-zero y has an inverse, as should be the case for field elements!
The roots of the reduction polynomial are not always linear independent and we can't use them as a basis, but it can be proven that there will always exist some element  such that (
such that (  ,
,  2,
2,  22, ...,
22, ...,  2m-1) is linear independent. Such a basis is called a normal basis.
2m-1) is linear independent. Such a basis is called a normal basis.
As an example, let the reduction polynomial again be t4 + t + 1. The set (t, t2, t4, t8) = (t, t2, t + 1, t2 + 1) is clearly not linear independent. However, we can chose  = t3 and find a normal basis (t3, t3 + t2, t3 + t2 + t + 1, t3 + t). If next we want to find the matrix that corresponds with Atx = tx (multiplication with t) then we have to first figure out how the basis elements are converted.
= t3 and find a normal basis (t3, t3 + t2, t3 + t2 + t + 1, t3 + t). If next we want to find the matrix that corresponds with Atx = tx (multiplication with t) then we have to first figure out how the basis elements are converted.
t(t3) = t4 = t + 1 = (t3 + t2) + (t3 + t2 + t + 1).
t(t3 + t2) = t3 + t + 1 = (t3) + (t3 + t2) + (t3 + t2 + t + 1).
t(t3 + t2 + t + 1) = t3 + t2 + 1 = (t3) + (t3 + t2 + t + 1) + (t3 + t).
t(t3 + t) = t2 + t + 1 = (t3) + (t3 + t2 + t + 1).
And thus we have
![\[ \begin{pmatrix} 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} = t \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} \]](form_1022_292.png)
Note that again Tr(t) = 0, as it should be. Lets have a look at an element whose trace will not be 0 for change, like t3. Using the above formula for the trace we can immediately calculate it.
![\[ Tr(t^3) = t^3 + t^6 + t^9 + t^{12} = t^3 + (t^3 + t^2) + (t^3 + t^2 + t + 1) + (t^3 + t) = 1 \]](form_1022_293.png)
Note that this is exactly the sum of the normal basis that we used above.
Lets do one more check with a matrix, using this same basis. The basis elements are converted as follows:
t3(t3) = (t3 + t2).
t3(t3 + t2) = (t3 + t).
t3(t3 + t2 + t + 1) = 1 = (t3) + (t3 + t2) + (t3 + t2 + t + 1) + (t3 + t).
t3(t3 + t) = (t3 + t2 + t + 1).
And thus we have
![\[ \begin{pmatrix} 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} = t^3 \begin{pmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{pmatrix} \]](form_1022_294.png)
and as expected, the trace of this matrix is 1.
We can make an interesting observation here. A vector relative to a normal basis (  ,
,  2,
2,  22, ...,
22, ...,  2m-1) allows us to denote every single element of the field of course, otherwise it wasn't a basis. The zero is always given by the vector (0, 0, 0, ..., 0), and thus it is impossible that the vector (1, 1, 1, ... 1), which corresponds to adding all elements of the normal basis, would be zero as well. Moreover, adding all elements of a normal basis means adding all the roots of
2m-1) allows us to denote every single element of the field of course, otherwise it wasn't a basis. The zero is always given by the vector (0, 0, 0, ..., 0), and thus it is impossible that the vector (1, 1, 1, ... 1), which corresponds to adding all elements of the normal basis, would be zero as well. Moreover, adding all elements of a normal basis means adding all the roots of  , it is equal to the trace of
, it is equal to the trace of  , and a trace is element of the base field and can therefore only be equal to 0 or 1 in our case! Hence, in order for (
, and a trace is element of the base field and can therefore only be equal to 0 or 1 in our case! Hence, in order for (  ,
,  2,
2,  22, ...,
22, ...,  2m-1) to be a normal basis we must have 0
2m-1) to be a normal basis we must have 0 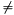 Tr(
Tr(  ) = 1 !
) = 1 !
Now consider the following magic. When  , in combination with Frobenius, can be used to form a normal basis, then so can
, in combination with Frobenius, can be used to form a normal basis, then so can  2 because if you replace
2 because if you replace  with
with  2 in the basis you simply get (
2 in the basis you simply get (  2,
2,  22, ...,
22, ...,  2m-1,
2m-1,  ). Therefore, it must be that Tr(
). Therefore, it must be that Tr(  2) = 1 too. The inverse is also true, if
2) = 1 too. The inverse is also true, if  2 can be used to generate a normal basis then so can
2 can be used to generate a normal basis then so can  . Hence, we can conclude that for any arbitrary element y
. Hence, we can conclude that for any arbitrary element y
![\[ Tr(y) = Tr(Frob(y)) \]](form_1022_296.png)
This result is not too weird, considering that Frobenius is an automorphism that basically just changes the basis - and as we saw before, the trace is not dependent on the basis.
In other words, Tr(y - Frob(y)) = Tr(y) - Tr(Frob(y)) = 0. And therefore we can conclude that the equation x = y + y2 can only have solutions when Tr(x) = 0 ! Note that Frob(y) = y2 and that, since we are working with characteristic 2, y + y2 = y - y2.
And this is the result I needed to prove Hypothesis 1.
PROOF
There is another, easy way to prove theorem 5. Suppose there is a solution to the equation x = y + y2, so that for a given x and y the equation is true. Then applying Frobenius to both sides (squaring both sides) results again in in an equation that is true of course. We can repeat squaring both sides precisely m - 1 times at which point the term y2 will turn into y because y2m = y. If we subsequently add up all those equations we get immedeate proof that the trace of x is 0.
![\[ \] \begin{eqnarray*} x &=& y + y^2 \\ x^2 &=& y^2 + y^4 \\ x^4 &=& y^4 + y^8 \\ \vdots \\ x^{2^{m-2}} &=& y^{2^{m-2}} + y^{2^{m-1}} \\ x^{2^{m-1}} &=& y^{2^{m-1}} + y \end{eqnarray*} \[ \]](form_1022_297.png)
where the sum of all left-hand-sides is precisely the trace of x and the sum of all right-hand-sides is zero!
Weew, you have no idea how glad I am that I finally got to this point without using sophisticated mathematics! I worked five days on the above. Hopefully I reached my goal and you are now reasonably comfortable with Frobenius and traces. Just for the kicks (and so you appreciate my efforts a bit more), here is the "sophisticated" derivation:
Let G be the Galois group of the Galois extension L/K, then  (Hilbert's theorem 90). Therefore, if G is cyclic with generator g, this is the same as Norm(x) = 1
(Hilbert's theorem 90). Therefore, if G is cyclic with generator g, this is the same as Norm(x) = 1  x = y/g(y). And Tr(x) = 0
x = y/g(y). And Tr(x) = 0  x = y - g(y).
x = y - g(y).
Also trace (of field elements) is usually explained with Galois theory. Maybe I'll add a chapter about Galois Theory later to this project.
A week after I wrote the above, I found emperically an extremely fast way to find the trace of an element of  . I showed this method on an IRC channel on 10 December 2004 and posted it to the sci.math news group on 11 December 2004. I managed to find a prove for it on 18 December 2004 (see below). Unfortunately, then I found a (yet unpublished) article on the net that proved the same thing (theorem 7 of On the Number of Trace-One Elements in Polynomial Bases for F2n).
. I showed this method on an IRC channel on 10 December 2004 and posted it to the sci.math news group on 11 December 2004. I managed to find a prove for it on 18 December 2004 (see below). Unfortunately, then I found a (yet unpublished) article on the net that proved the same thing (theorem 7 of On the Number of Trace-One Elements in Polynomial Bases for F2n).
Although we found this independently, and although the other article will probably not be published before 2005, I suppose I can't publish it myself anymore; too bad.
THEOREM 6

 with reduction polynomial tm + tk0 + tk1 +
with reduction polynomial tm + tk0 + tk1 +  + tkn + 1, where each ki < m / 2. Then the trace of tj is 1 iff j is odd and there exists an i such that j = m - ki, or when j = 0 and m is odd.
+ tkn + 1, where each ki < m / 2. Then the trace of tj is 1 iff j is odd and there exists an i such that j = m - ki, or when j = 0 and m is odd.Please give me credit if you use it anywhere.
PROOF
We start this proof with a repetion of the theory of eigenvalues and the trace, but slightly more rigorous because we need that to understand how the eigenvalues of a power of t relates to the eigenvalues of t.
Let  be the degree m extension field of
be the degree m extension field of  2. Then
2. Then  =
=  2[t]/(r(t)) where r(t) is an irreducible polynomial of degree m over
2[t]/(r(t)) where r(t) is an irreducible polynomial of degree m over  2. The element
2. The element  = t is a root of r(t) in
= t is a root of r(t) in  , and { 1,
, and { 1,  ,
,  2, ...,
2, ...,  m-1 } is a basis for
m-1 } is a basis for  over
over  2, called the polynomial basis. The trace of an element x
2, called the polynomial basis. The trace of an element x 
 was shown before to be
was shown before to be  .
.
Simultaneously,  is a vector space V of dimension m over
is a vector space V of dimension m over  2. And the element x can be considered to be a linear transformation x: V
2. And the element x can be considered to be a linear transformation x: V  V, representing multiplication with x, carrying any element y to xy. Using the polynomial basis, let T be the matrix that carries any element y to ty. Thus, Ty = ty for any vector y
V, representing multiplication with x, carrying any element y to xy. Using the polynomial basis, let T be the matrix that carries any element y to ty. Thus, Ty = ty for any vector y  V and where t is the special element as defined by the reduction map. Then T has the general form
V and where t is the special element as defined by the reduction map. Then T has the general form
![\[ \begin{pmatrix} 0 & 1 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 1 & \ddots & \vdots \\ 0 & \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ r_0 & r_1 & r_2 & r_3 & \cdots & r_{m-1} \\ \end{pmatrix} \]](form_1022_301.png)
where the ri 
 2 are the coefficients of the reduction polynomial r(t) = tm + rm-1tm-1 + ... + r1 t + r0. Note that always r0 = 1 or the reduction polynomial would not be irreducible.
2 are the coefficients of the reduction polynomial r(t) = tm + rm-1tm-1 + ... + r1 t + r0. Note that always r0 = 1 or the reduction polynomial would not be irreducible.
Also note that the trace of this matrix (the sum of the diagonal elements), and thus of t, equals rm-1 (a well-known fact, as is proven for example by Bhargav (lemma 3.2)), Tr(t) = rm-1.
The characteristic polynomial of a linear transformation T is defined as f(e) = det(T - eI), where I is the identity matrix. Obviously it has coeficients in  2, the ground field of V. The equation f(e) = 0 has a solution if and only if (T - eI)(v) = 0 for some nonzero vector v; in general, for any linear transformation A, det(A) = 0 if and only if Av = 0 is satisfied by a nonzero vector v. We are taking the special case of A = (T - eI). Now note that (e, v) is an eigenvalue - eigenvector pair of T if and only if Tv = ev, which is true if and only if (T - eI)(v) = 0. e is an eigenvalue of T if and only if f(e) = 0, where f is the above mentioned characteristic polynomial.
2, the ground field of V. The equation f(e) = 0 has a solution if and only if (T - eI)(v) = 0 for some nonzero vector v; in general, for any linear transformation A, det(A) = 0 if and only if Av = 0 is satisfied by a nonzero vector v. We are taking the special case of A = (T - eI). Now note that (e, v) is an eigenvalue - eigenvector pair of T if and only if Tv = ev, which is true if and only if (T - eI)(v) = 0. e is an eigenvalue of T if and only if f(e) = 0, where f is the above mentioned characteristic polynomial.
Now let T again be the matrix that carries an element y to ty. Then we will show that the characteristic polynomial of T, f(e), is precisely the reduction polynomial r and thus e will be an eigenvalue of T if and only if r(e) = 0, and the eigenvalues of T turn out to be the roots of the reduction polynomial.
The characteristic polynomial of T is det(T - eI) is
![\[ \left| \begin{matrix} -e & 1 & 0 & 0 & \cdots & 0 \\ 0 & -e & 1 & 0 & \cdots & 0 \\ 0 & 0 & -e & 1 & \ddots & \vdots \\ 0 & \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & 0 & -e & 1 \\ r_0 & r_1 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| \]](form_1022_302.png)
It is easy to see that this determinant is the reduction polynomial because it is equal to
![\[ -e \left| \begin{matrix} -e & 1 & 0 & \cdots & 0 \\ 0 & -e & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & -e & 1 \\ r_1 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| - 1 \cdot \left| \begin{matrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & -e & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & -e & 1 \\ r_0 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| \]](form_1022_303.png)
and the second underdeterminant can be worked out to
![\[ \left| \begin{matrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & -e & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & -e & 1 \\ r_0 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| = -1 \cdot \left| \begin{matrix} 0 & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & 0 & -e & 1 \\ r_0 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| = \cdots = (-1)^{m-3} \left| \begin{matrix} 0 & 1 \\ r_0 & r_{m-1} - e \end{matrix} \right| = (-1)^{m-2} r_0 \]](form_1022_304.png)
and thus
![\[ \left| \begin{matrix} -e & 1 & 0 & 0 & \cdots & 0 \\ 0 & -e & 1 & 0 & \cdots & 0 \\ 0 & 0 & -e & 1 & \ddots & \vdots \\ 0 & \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & 0 & -e & 1 \\ r_0 & r_1 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| = -e \left| \begin{matrix} -e & 1 & 0 & \cdots & 0 \\ 0 & -e & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & 0 & -e & 1 \\ r_1 & r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| + (-1)^{m-1} r_0 \]](form_1022_305.png)
then use this formula recursively to find that this is equal to
![\[ (-1)^2 e^2 \left| \begin{matrix} -e & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & 0 & -e & 1 \\ r_2 & r_3 & \cdots & r_{m-1} - e \end{matrix} \right| -e (-1)^{m-2} r_1 + (-1)^{m-1} r_0 = \cdots = (-1)^{m-1} r(e) \]](form_1022_306.png)
Ok, almost equal then. However, in our case with characteristic 2, the -1 is congruent 1 and in any case the equation r(e) = 0 remains the equation that needs to be satisfied in order for e to be an eigenvalue of T.
We already have one root of the characteristic polynomial of T therefore, because r(t) = 0 by definition. As was shown before, the other roots of the reduction polynomial can be obtained by applying Frobenius m - 1 times and we find that the eigenvalues of T are e  { t, t2, t4, ..., t2m-1 }. Note that the eigenvector v that belongs to a given eigenvalue e is (1 e e2 e3 ... em-1)T (and any vector that can be obtained by multiplying this vector with a non-zero scalar of course; there will be 2m - 1 different vectors that satisfy Tv = ev).
{ t, t2, t4, ..., t2m-1 }. Note that the eigenvector v that belongs to a given eigenvalue e is (1 e e2 e3 ... em-1)T (and any vector that can be obtained by multiplying this vector with a non-zero scalar of course; there will be 2m - 1 different vectors that satisfy Tv = ev).
The trace of a linear transformation T is known to be equal to the sum of the eigenvalues of T. So, we find again that  . Note that the norm of T (its determinant) is known to be equal to the product of the eigenvalues of T. And thus we have =
. Note that the norm of T (its determinant) is known to be equal to the product of the eigenvalues of T. And thus we have =  = t(2m-1) = 1.
= t(2m-1) = 1.
Now we are ready to look new things.
Consider the matrix Tn, then it is obvious that this matrix will have the exact same eigenvectors as T; for the eigenvalue-eigenvector pair (e, v) of T we find that Tn v = en v and thus v is an eigenvector of Tn with eigenvalue en.
From this we can conclude that the trace of tn equals the sum  . Note that when t is a generator of the field so that any x
. Note that when t is a generator of the field so that any x 
 can be written as a power of t, then we arrive again at the general formula for the trace of a field element
can be written as a power of t, then we arrive again at the general formula for the trace of a field element  . If the field is not primitive (t is not a generator), then we just have to find some generator g and use (g, g2, g3, ..., gm-1) as basis and will get the same result. And while we're at it, also note that =
. If the field is not primitive (t is not a generator), then we just have to find some generator g and use (g, g2, g3, ..., gm-1) as basis and will get the same result. And while we're at it, also note that =  = n = 1.
= n = 1.
We found above that the eigenvalues of T are precisely the roots of the reduction polynomial. That means that we can write the reduction polynomial as
r(t) = (t - e1)(t - e2)  (t - em)
(t - em)
Where the ei, the m eigenvalues of T, are the zeros. Expanding and using induction, we see that
r(t) = tm - S1tm-1 + S2tm-2 +  + (-1)mSm
+ (-1)mSm
Or, since we have characteristic 2,
r(t) = tm + S1tm-1 + S2tm-2 +  + Sm
+ Sm
where the Si are the Elementary Symmetric Polynomials of the m variables e1, e2, ..., em.
Moreover, using the fact that  , we can write
, we can write
Tr(tn) = Nn
where the Nn are the Newton Symmetric Polynomials of the m variables e1, e2, ..., em.
If we restrict ourselfs to reduction polynomials of the form tm + tk0 + tk1 +  + tkn + 1, where each ki
+ tkn + 1, where each ki  m / 2, then the first floor((m - 1) / 2) ESP's are zero.
m / 2, then the first floor((m - 1) / 2) ESP's are zero.
Using the fact that the characteristic of the field is 2, the relationship between NSP's and ESP's becomes
![\[ N_n = nS_n + \sum_{i=1}^{n-1} S_iN_{n-i} \]](form_1022_312.png)
From this we see immediately that, since Si = 0 for all i  floor((m - 1) / 2), also Ni = 0 for all i
floor((m - 1) / 2), also Ni = 0 for all i  floor((m - 1) / 2). Whence the sum
floor((m - 1) / 2). Whence the sum  is zero for any value n < m.
is zero for any value n < m.
For example, when m = 6 (even m is most critical) then only the first two ESP's and NSP's are garanteed zero: S1 = S2 = N1 = N2 = 0. And the sum exists of a maximum number of terms when n is maximum, n = m - 1 = 5, resulting in the sum  = S1N4 + S2N3 + S3N2 + S4N1 = 0.
= S1N4 + S2N3 + S3N2 + S4N1 = 0.
In other words, again remembering that the characteristic is 2, we find that for any 0 < n < m
![\[ Tr(t^n) = N_n = \begin{cases} 0 & \text{ n is even } \\ S_n & \text{ n is odd } \end{cases} \]](form_1022_314.png)
This doesn't cover n = 0, but we already know that Tr(1) = 1 iff m is odd.
QED